5.12 Exploring Behaviors of Implicit Relations
6 min read•june 18, 2024
AP Calculus AB/BC ♾️
279 resourcesSee Units
Overview
We know that a function's derivative can be used to understand the behavior of a function. This holds true for implicit functions too! An implicit function is a type of function that is not defined in the usual way, with an independent variable and a dependent variable. Instead, an implicit function is defined by an equation that relates multiple variables. But you can justify conclusions about the behavior of an implicitly defined function based on evidence from its derivatives.
Here are some basic steps to help you get started
- Find the equation that defines the implicit function. For example, if the function is defined by the equation x^2 + y^2 = 1, the equation is x^2 + y^2 = 1.
- Differentiate the equation with respect to x. This will give you the derivative of the function in implicit form.
- Solve the derivative equation for dy/dx. This will give you an expression for the derivative of the function in terms of x and y.
- Substitute values for x and y into the derivative expression to find the derivative at specific points.
- Analyze the derivative to understand how the function is changing at each point. For example, if the derivative is positive, the function is increasing at that point. If the derivative is negative, the function is decreasing at that point.
Here's an example to illustrate these steps:
Consider the implicit function defined by the equation
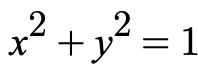
To find the derivative of this function, we differentiate the equation with respect to x:

Solving for dy/dx, we get:
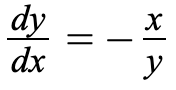
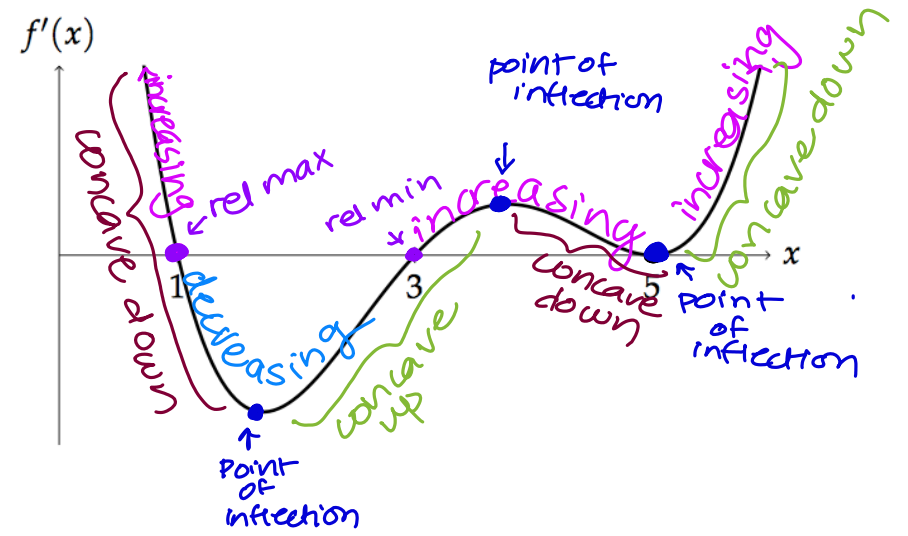
Now, we have a derivative that we can graph and use to analyze the function using the same rules that we use for regular functions. As a reminder:
- If f'(x) is positive, then the graph of f(x) is increasing
- If f'(x) is negative, then the graph of f(x) is decreasing
- If f'(x) is decreasing, then the graph of f(x) is concave down
- If f'(x) is increasing, then the graph of f(x) is concave up
- If f'(x) changes from positive to negative at x=k, then f(x) has a relative maximum at x=k
- If f'(x) changes from negative to positive at x=k, then f(x) has a relative minimum at x=k
Let's practice this using the graph of dy/dx = -x/y
We can plug in some different points to help us analyze the behavior. For example, if we use the point (1,1), we find that dy/dx=-1. Using the rules we outlined above, this tells us that the first derivative is negative and therefore the function is decreasing at that point.
In this case, we want to use the derivative to find all characteristics of the graph, so we will set the dy/dx equal to 0 and solve for any possibilities for 0 or undefined. These are our critical points and are what we'll use to find all the characteristics of the function.
-x/y=0
In this example, both x and y could be equal to 0 in order to make the entire derivative 0. We would plug both of these values into the original equation to find the ordered pair and describe the function at that point.
Let's look at an example
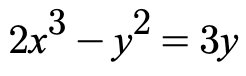
This is an implicit function that looks like the following when graphed
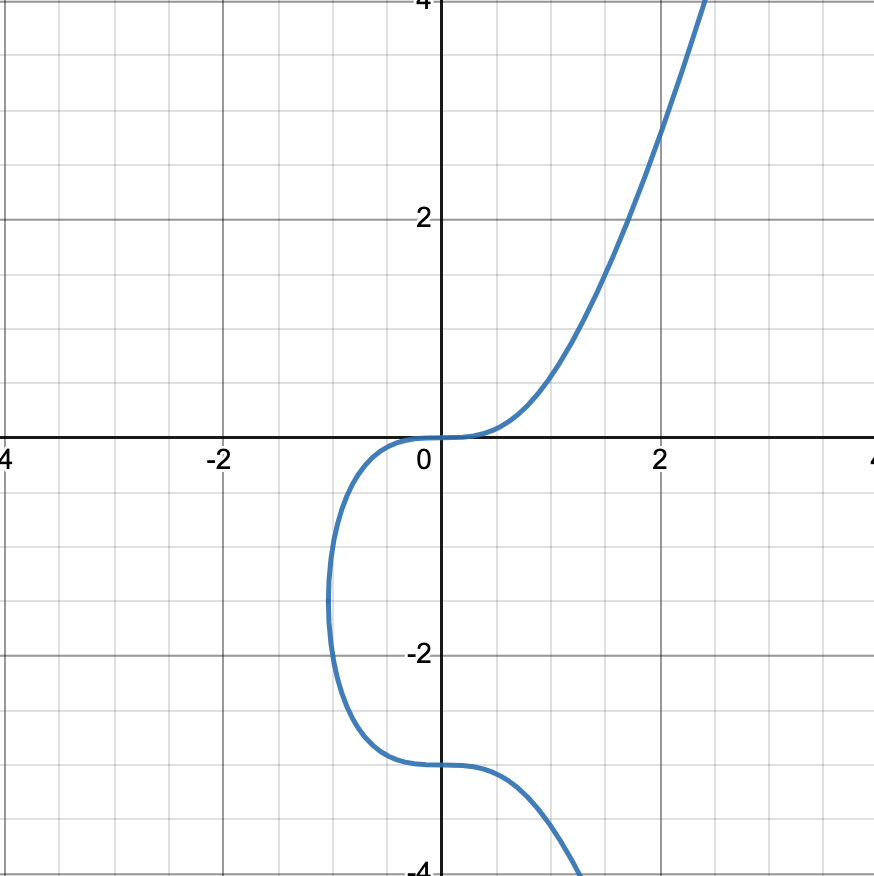
In order to differentiate this equation, we must derive it with respect to x. This leaves us with
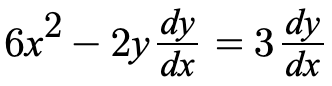
We can then solve for dy/dx

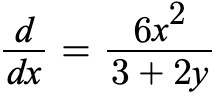
Now, we can test points that will tell us information about the function. If we test the point (3,3), dy/dx is positive, which tells us that the function is increasing at that point. If we test the point (0,0), dy/dx is equal to 0, telling us that the function is neither increasing nor decreasing at that point. These correspond to the picture of the function above.
Tips and reminders
Oftentimes, the difficult part of analyzing implicit functions is not the analysis but rather the implicit differentiation. This is really important because these ideas from implicit differentiation will continue to be used in later units, so it's crucial to understand! Remember these helpful tips:
- Remember that implicit differentiation involves taking the derivative of an equation, rather than an expression. This means that you need to differentiate both sides of the equation with respect to the variable you are trying to find the derivative of.
- Use the chain rule when differentiating composite functions. For example, if you have an equation of the form f(g(x)), the derivative of this with respect to x is f'(g(x))*g'(x).
- Be careful when differentiating equations involving fractional expressions. In these cases, it can be helpful to use the quotient rule to take the derivative of the fraction.
- Don't forget to use the product rule when differentiating products of functions.
- Make sure to use the correct notation for derivatives. The derivative of a function f with respect to a variable x is denoted by f'(x) or df/dx.
- Use the fact that the derivative of a constant is zero. This can help you simplify your final answer.
- Practice solving a variety of implicit differentiation problems. The more you practice, the more comfortable you will become with the process.
There are also some common misconceptions. One common misconception about analyzing the first derivative of implicit differentiable equations is that the derivative can be found by simply differentiating both sides of the equation with respect to the independent variable. However, this is not always the case for implicit equations.
For example, in the equation

If we try to differentiate this equation with respect to x, we get
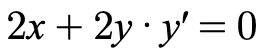
This does not give us a straightforward expression for y'. In order to find the derivative of an implicit equation, we must first solve for one of the variables in terms of the other and then differentiate with respect to the independent variable.
Another misconception is that the derivative of an implicit equation is always equal to the derivative of an equivalent explicit equation. This is not always true, as the derivative of an implicit equation may not simplify to the same form as the derivative of an explicit equation.
For example, consider the implicit equation

and the explicit equation y = sqrt(1 - x^2).
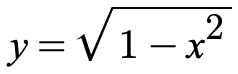
While these equations are equivalent, their derivatives are not. The derivative of the implicit equation is 2x + 2yy' = 0, while the derivative of the explicit equation is -2xx'. These two derivatives are not equivalent, even though the original equations were.
A third misconception is that the first derivative of an implicit equation is always equal to the slope of the curve described by the equation. While this may be true for some implicit equations, it is not always the case. The derivative of an implicit equation gives the rate of change of one variable with respect to the other, not necessarily the slope of the curve.
For example, consider the implicit equation

The derivative of this equation with respect to x is 3x^2 + 3xyy' = 0, which does not give us a straightforward expression for the slope of the curve. In order to find the slope of the curve, we must solve for one of the variables in terms of the other and then take the derivative with respect to the independent variable.
In summary, it is important to be aware of these common misconceptions when analyzing the first derivative of implicit differentiable equations. It is not always possible to simply differentiate both sides of the equation, and the derivative of an implicit equation may not simplify to the same form as the derivative of an explicit equation or equal the slope of the curve described by the equation.
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.