AP Calculus AB/BC ♾️
279 resourcesSee Units
Answers and Review for Multiple Choice Practice on Analytical Applications of Differentiation
⛔STOP!⛔ Before you look at the answers make sure you gave this practice quiz a try so you can assess your understanding of the concepts covered in unit 1. Click here for the practice questions: AP Calculus Unit 5 Multiple Choice Questions. Facts about the test: The AP Calculus exam has two sections of multiple choice: 30 questions in 60 minutes with no calculator, and 15 questions in 45 minutes with a calculator. *The following questions were not written by CollegeBoard and although they cover information outlined in the AP Calculus Course and Exam Description the formatting on the exam may be different.
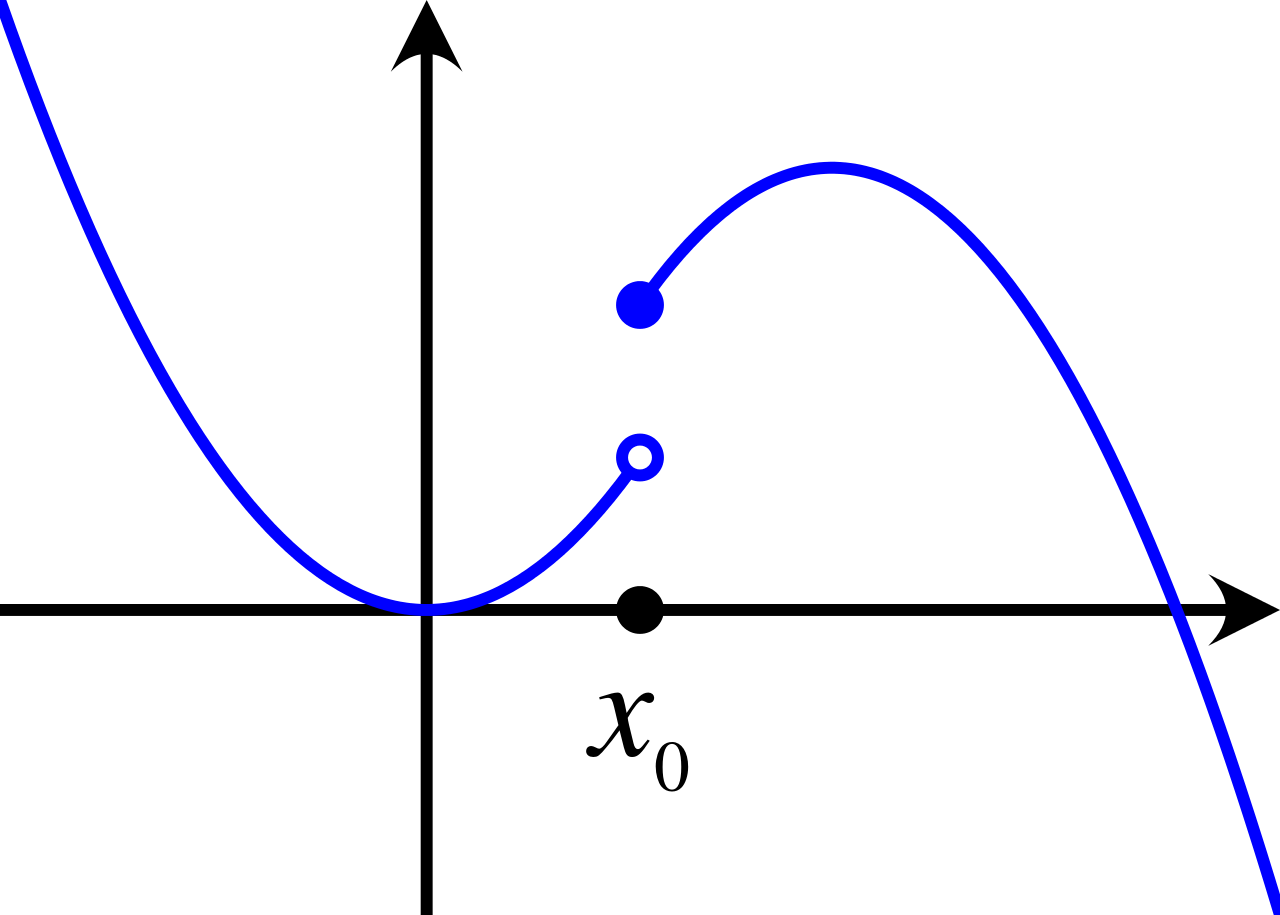
1.
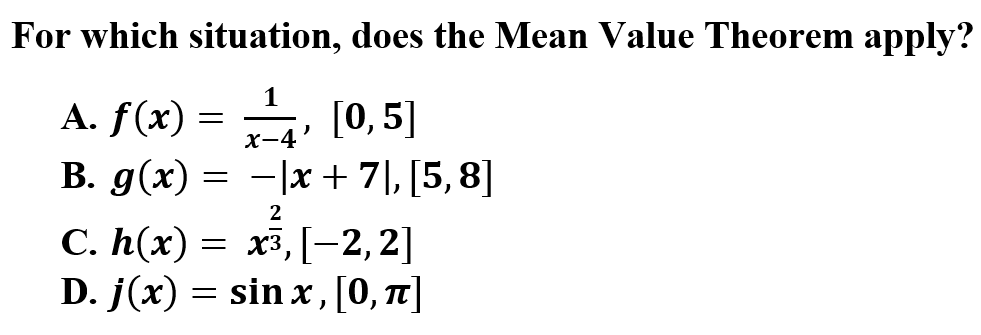
D is correct because Mean Value Theorem can be utilized when a function is continuous and has a closed interval. Each graph needs to be tested to determine continuity on the interval given.
2.
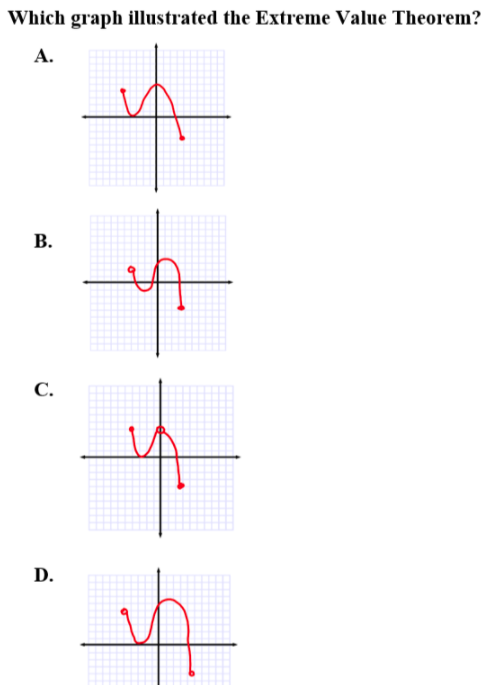
A is correct because Extreme Values Theorem guarantees one minimum and one maximum value on a continuous function on a closed interval. Each graph is not continuous and on a closed interval except choice A.
📄 Study Unit 5.2: Extreme Value Theorem, Global vs Local Extrema, and Critical Points
3.
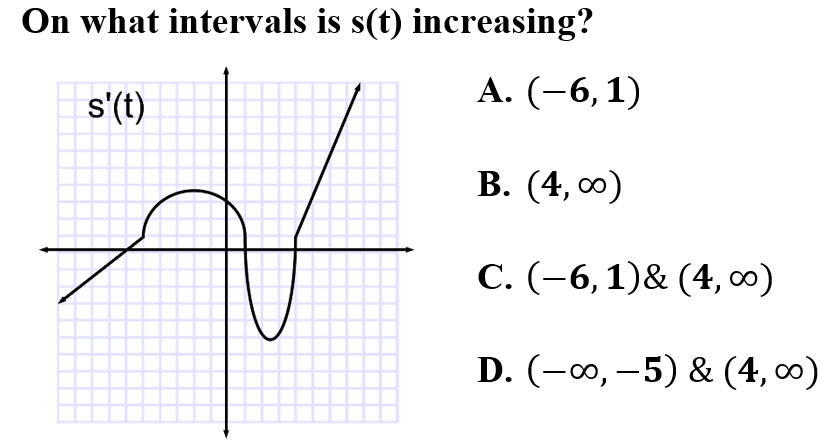
C is correct because using the graph of the first derivative, intervals of increasing can be seen where the derivative is above the x-axis. Other behaviors are indicative of characteristics that do not involve the intervals of increasing.
📄 Study Unit 5.3: Determining Intervals on Which a Function is Increasing or Decreasing
4.
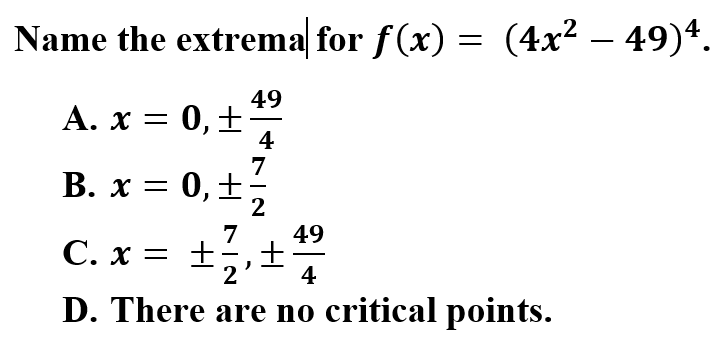
B is correct because to determine extrema, utilize the First Derivative Test. Once the you have determined f'(x), you will need to set equal to zero and solve.
📄 Study Unit 5.4: Using the First Derivative Test to Determine Relative (Local) Extrema
5.

A is correct because to determine intervals of increasing and decreasing, one can take the derive of the function. Using derivatives of trigonometric functions and the chain rule the derivative matches choice A and B. We can narrow the solution to choice A because the sign chart gives the negative values.
📄 Study Unit 5.4: Using the First Derivative Test to Determine Relative (Local) Extrema
6.
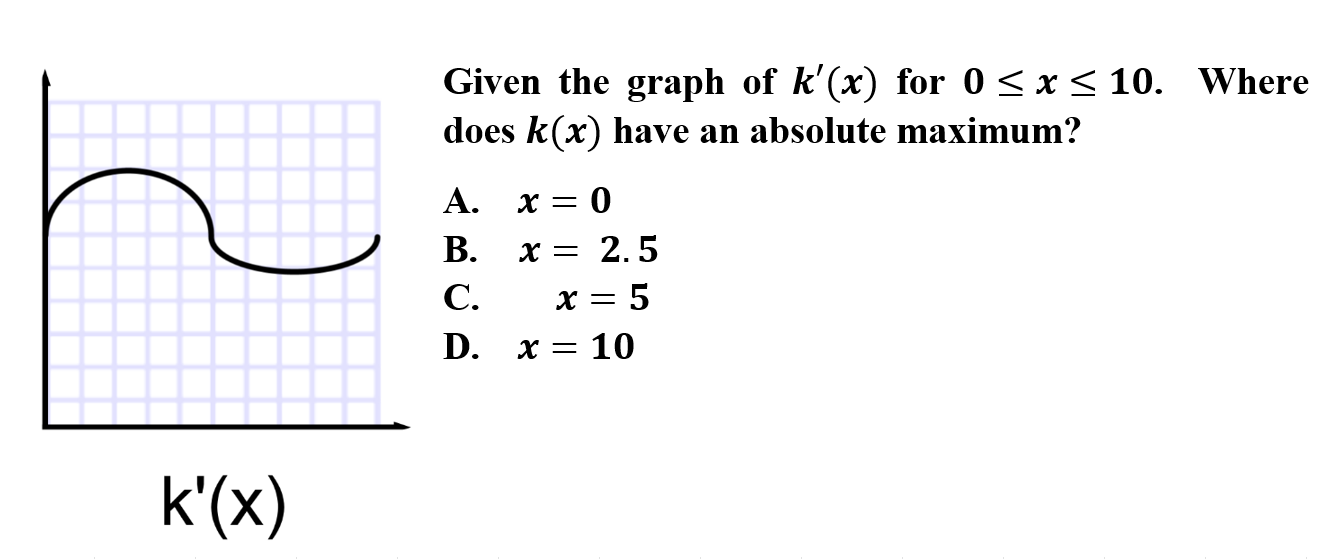
D is correct because since k(x) is continuous, you can utilize the Extreme Value Theorem. If needed, k(x) is also on a closed interval, which allows usage of the Candidates Test. Since k'(x) is above the x-axis, k(x) is always increase. The absolute maximum would be at the highest point which is x = 10.
📄 Study Unit 5.2: Extreme Value Theorem, Global vs Local Extrema, and Critical Points
7.
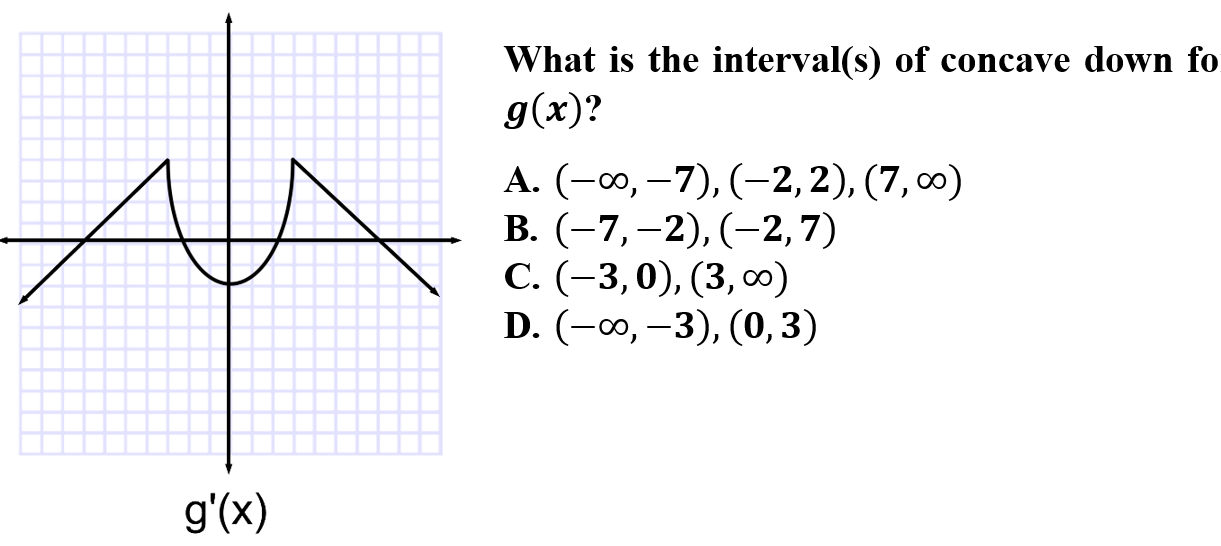
C is correct because when given g'(x), concavity can be determined where the graph is decreasing. Remember to always determine the type of graph (or information) given before establishing your solution.
📄 Study Unit 5.6: Determining Concavity
8.

A is correct because to determine concavity with a given function, you must obtain the second derivative and determine the critical point(s). Once you have the critical point(s), you can utilize a sign chart to determine the positive values which will result in concave up.
9.

D is correct because Points of Inflections are defined as the changes of concavity of a function. Concavity can be determined using the the intervals of increasing/decreasing or extrema of the first derivative. Concavity can be determined using the change of signs between critical points of a second derivative.
10.
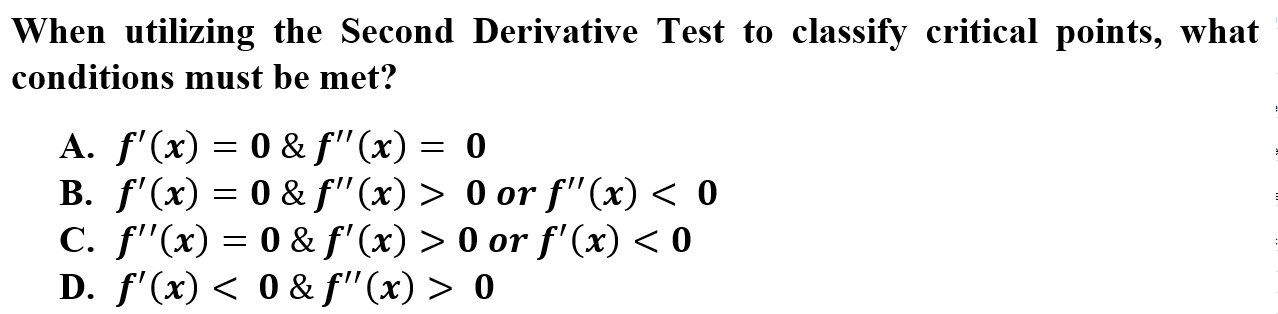
B is correct because The Second Derivative Test can be utilized when the function has a critical point and the second derivative is defined as positive or negative. If the first is undefined at x or the second is zero at x, the Second Derivative is not applicable.
11.

C is correct because the table indicates values where f(x) are negative and getting more negative. This would indicate a f'(x) < 0 and f''(x) > 0.
📄 Study Unit 5.6: Determining Concavity
12.

B is correct because given the first derivative, extrema are found where it crosses the x=axis. Maximums are where the first derivative goes from positive to negative and minimums are where the first derivative goes from negative and positive. Concavity can be found where the first derivative is increasing and decreasing.
📄 Study Unit 5.6: Determining Concavity
13.

A is correct because optimization are problems where a maximum/minimum of a situation needs to be found. Once you have a function with one variable. you will need to find the critical points and utilize the Candidates Test to determine the absolute maximum/minimum.
14.

C is correct because the equation must be derived implicitly. In implicit differentiation, all rules of derivatives can be utilized. In this case, you will implement the power, product, and constant rule.
15.

B is correct because given the function and its derivatives, to determine the behavior of the graph you need to substitute. First, substitute x = 1 in the function to determine the point. Then, plug in point to first and second derivative and interpret the results.
📄 Study Unit 5.6: Determining Concavity
What can we help you do now?
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
🧐Multiple Choice Questions (MCQ)
✍️Free Response Questions (FRQ)
📆Big Reviews: Finals & Exam Prep

Fiveable
Resources
© 2023 Fiveable Inc. All rights reserved.