AP Calculus AB/BC ♾️
279 resourcesSee Units
Answers and Review for Multiple Choice Practice on Integration and Accumulation of Change
⛔STOP!⛔ Before you look at the answers make sure you gave this practice quiz a try so you can assess your understanding of the concepts covered in unit 1. Click here for the practice questions: AP Calculus Unit 6 Multiple Choice Questions. Facts about the test: The AP Calculus exam has two sections of multiple choice: 30 questions in 60 minutes with no calculator, and 15 questions in 45 minutes with a calculator. *The following questions were not written by CollegeBoard and although they cover information outlined in the AP Calculus Course and Exam Description the formatting on the exam may be different.
1.
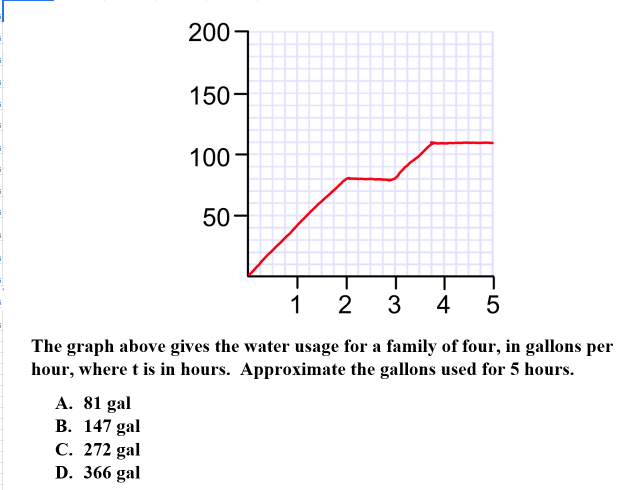
Explanation: D is correct because to approximate areas, you can divide the graph into common shapes (triangles, rectangles, etc.). Once you have the parts of the graph, you can add the areas to gain the approximation of the area under the graph.

Explanation: A is correct when utilizing the left Riemann Sums, you start will the initial values and end at i-1. Therefore, the end point is not used to approximate the area when using Left Riemann Sums.
3.

Explanation: B is correct because the right Riemann Sums will start with the second value once you determine delta x. It will end with the upper bound.
4.

Explanation: A is correct because once you have determined the values needed from delta x, you can pull the values from the table. You will find the individual area and add the values together.
5.
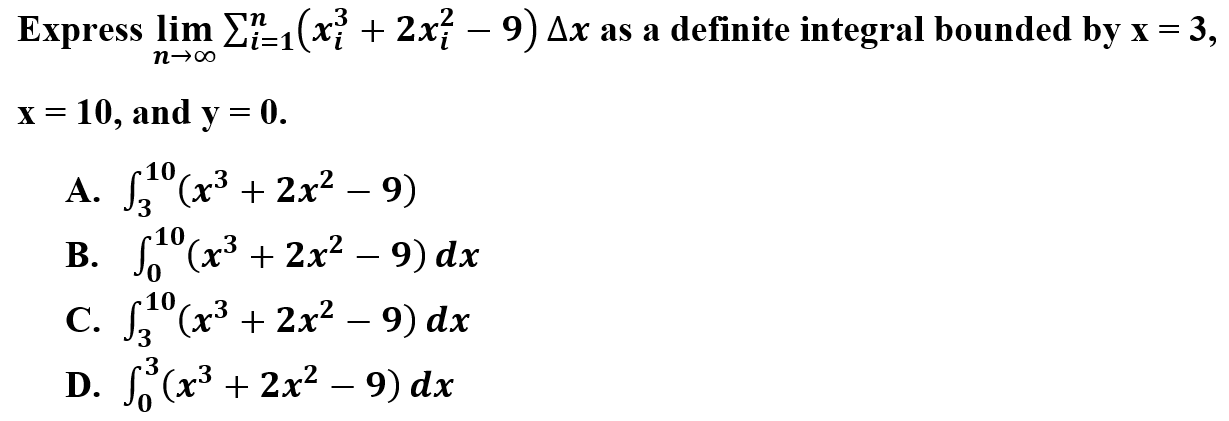
Explanation: C is correct because when summations are expressed as limits, the format can be expressed as a definite integral. The function in the summation can be converted into a function within the definite integral with the upper and lower bound.
6.
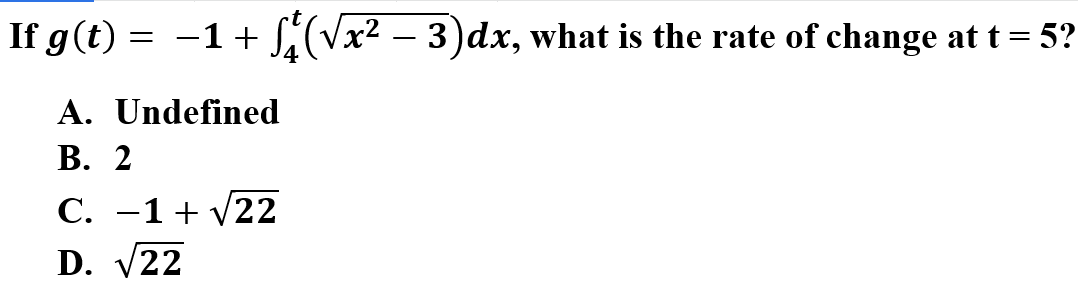
Explanation: D is correct because remember rate of change is derivative. Therefore, take the derivative of the integral which will cause the constant to go to 0. Then plug in t = 5 into the derivative of the integral.
7.
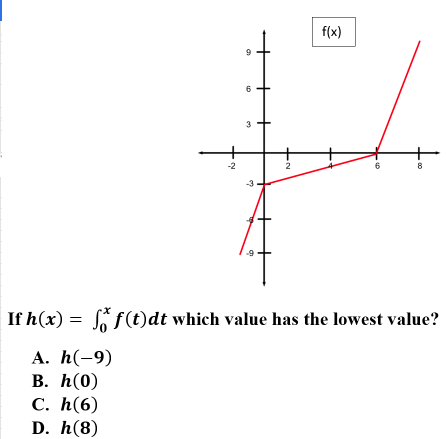
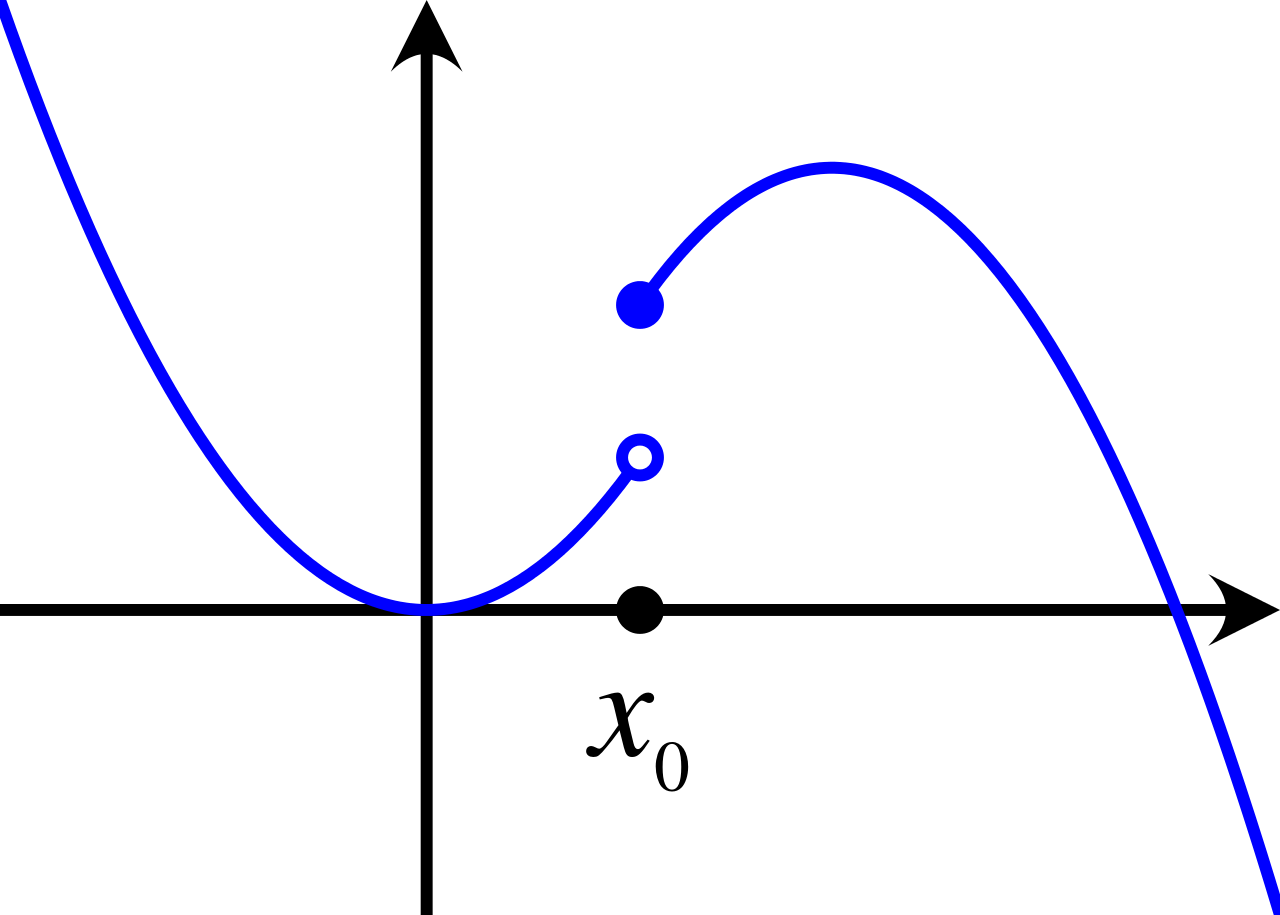
Explanation: C is correct because the graph is the derivative of h(x). Graphs of derivatives can be used to locate minimums where there it crosses the x-axis and there is a change of sign from negative to positive.
8.
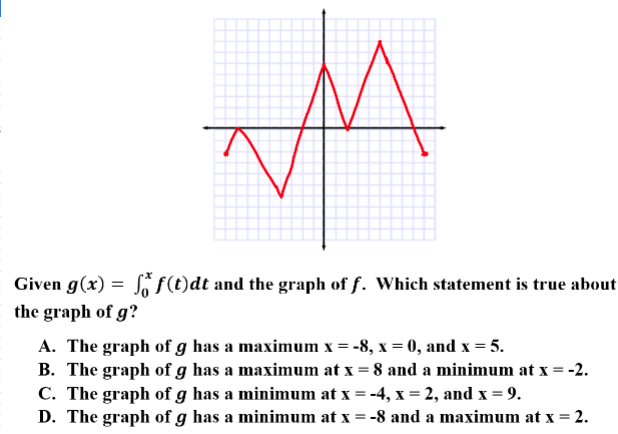
Explanation: B is correct because graphs of derivatives show extrema when g'(x) = f(x) = 0. There must be a change of sign. Points which are on the x-axis but do not change signs are not minimums/maximums.
9.
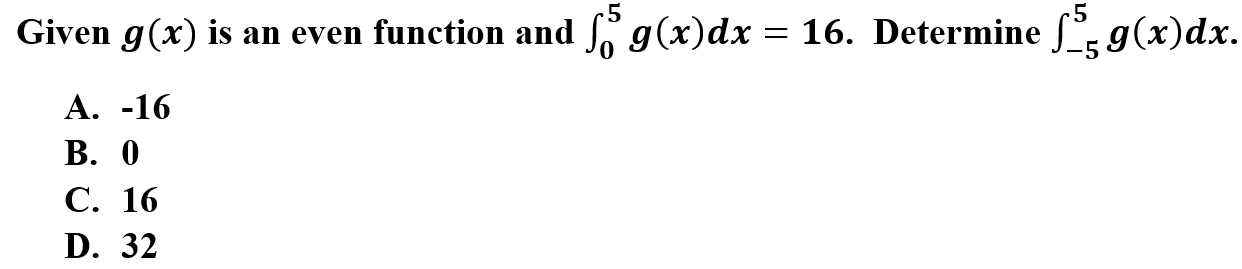
Explanation: D is correct because the definite integrals of an even function on [-5, 5] can be found by doubling the integral on [0, 5]. Since the integral on [0, 5] is given, the solution is found by 2 * 16 = 32.
10.
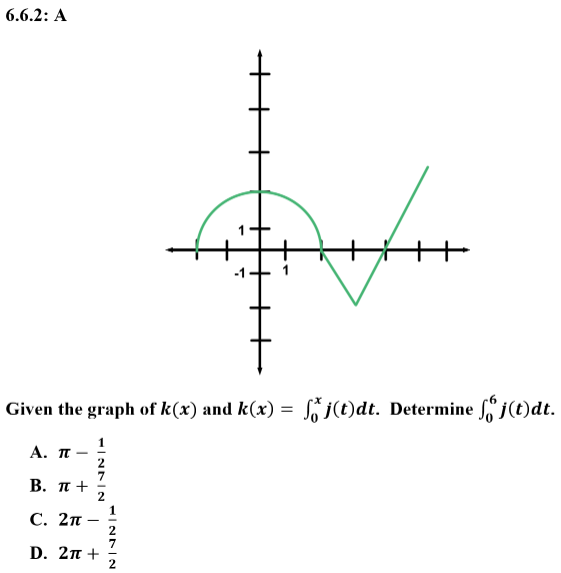
Explanation: A is correct because the definite integral can be determined by utilizes common geometric shapes and their area. In this problem, 1/4 of a circle is used and triangles are used. Be sure to remember those shapes under the x-axis are negative.
11.

Explanation: B is correct because integrations are the opposite of derivatives. By practicing derivatives, you will remember the integration of this integral is the reverse of the power rule. Then substitute the values into the function and subtract.
12.

Explanation: D is correct because you need to understand the integration of a derivative is the function. Therefore, once the integration is taken you can pull the information from the f(x) line of the table.
13.
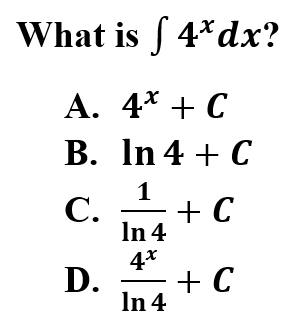
Explanation: D is correct because this is a basic integration rule. There are several rules you must know cold. Be sure to memorize and practice the integration/derivative rules.
📄 Study Unit 6: Integration and Accumulation of Change
14.
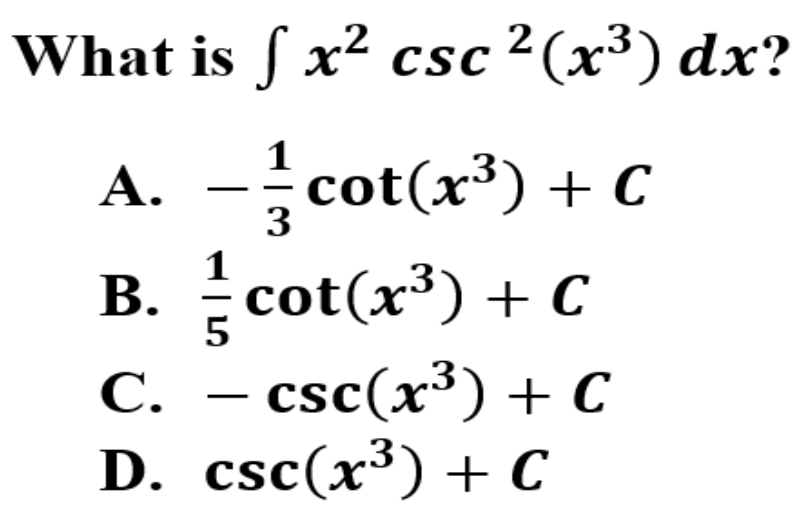
Explanation: A is correct because in this antiderivative, the derivative is only partially present. You must include the 1/3 to be able to include 3 to the derivative. Remember to know the integration/derivative rules cold.
15.
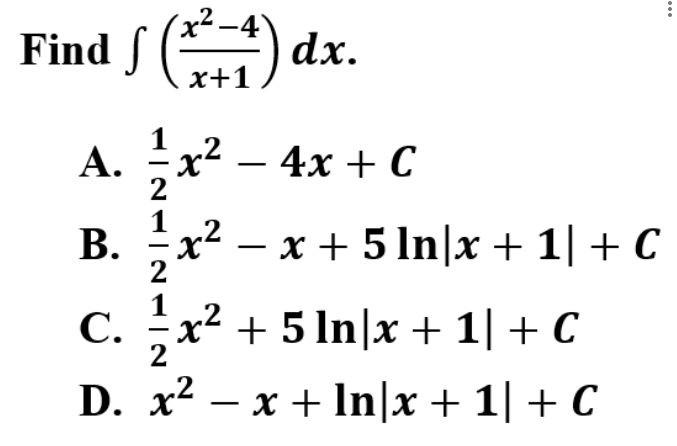
Explanation: B is correct because rational functions can be simplified by using long division. Once you complete long division, the remainder (5) becomes the most difficult part. The rest is a simple power rule.
What can we help you do now?
🤝Connect with other students studying AP Calculus with Hours
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
🧐Multiple Choice Questions (MCQ)
✍️Free Response Questions (FRQ)
📆Big Reviews: Finals & Exam Prep

Fiveable
Resources
© 2023 Fiveable Inc. All rights reserved.