📚

All Subjects

🧪

AP Chem

🔥

Unit 6

6.4 Heat Capacity and Calorimetry

7 min read•june 18, 2024

Dylan Black

Dalia Savy

Anika P

AP Chemistry 🧪

269 resources

See Units

Calorimetry

The absolute enthalpy of a system (H) cannot be measured directly, but changes in enthalpy (ΔH) can be measured using calorimetry. Calorimetry is the study of heat flow and heat exchange between a system and its surroundings and it can be used to calculate ΔH by measuring changes in temperature, which represent heat being lost or gained.

Types of Calorimeters

Calorimetry is a process by which a reaction takes place in a controlled vessel in which there is a liquid (typically water) and a temperature gauge like a thermometer to measure how the liquid heats up. There are several types of calorimeters that can be used to measure the heat flow in a chemical reaction or physical process:

In a bomb calorimeter, a reaction takes place in a sealed container, called a bomb, and the heat generated by the reaction is used to raise the temperature of the surrounding water. By measuring the rise in temperature of the water and knowing its specific heat, the heat of the reaction can be calculated.
In a constant-pressure calorimeter, the heat of a reaction is measured by monitoring the change in temperature of the reaction mixture at a constant pressure. This is because at constant pressure, the amount of heat transferred to a system is equal to ΔH.
In a coffee-cup calorimeter, which is a simple calorimeter, the heat released or absorbed by a reaction is used to raise or lower the temperature of the surrounding water. By measuring the temperature change of the water and knowing its mass and specific heat, the heat of the reaction can be calculated. Coffee-cup calorimetry is going to be our focus in this unit, and we will learn how to use it to observe changes in energy.

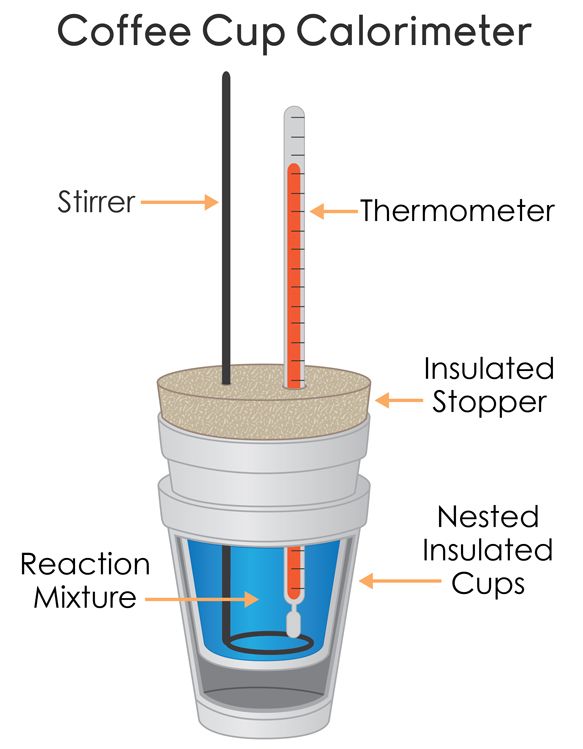
Coffee-Cup Calorimetry

We have a few parts to this coffee-cup calorimeter:

The thermometer🌡️
The reaction mixture
The stirrer to stir the reaction mixture and allow for more accurate temperature measurements.
An insulated container (such as a styrofoam cup)
Heat-proof lid to cover the calorimeter

The calorimeter is meant to insulate the sample, meaning that heat cannot come in or out of the system. The more insulated, the better the understanding of heat changes during a chemical reaction📏.

Quantifying Energy

The First Law of Thermodynamics

Since a calorimeter is insulated, we can think of it as an isolated system where the First Law of Thermodynamics is significant. To recall, it states that energy cannot be created or destroyed, only transferred or converted from one form to another. This means that the total amount of energy in the closed calorimeter remains constant over time.

👉 Need a quick review of this fundamental principle of chemistry and physics? Check out our study guide discussing endothermic and exothermic processes, featuring this concept.

Measuring Heat Transferred

Okay, so let's back up. Now, we know of a technique we can use to measure how much energy is absorbed or released during a chemical reaction. When we need to quantify this transfer of energy, we can use coffee-cup calorimetry and allow the chemical reaction to occur in the calorimeter.

Once the chemical reaction occurs, we can use the equation q=mCΔT to quantify the magnitude of heat transferred between the system and its surroundings in a calorimeter. Let's break it down:

q is the heat in Joules
m is the mass in grams or kilograms
C is the specific heat of the substance, and
ΔT is the change in temperature in Kelvin

In most questions, you are going to be solving for q. Regardless, you should be mindful of the units of each of these components. Note that because Celcius and Kelvin are equivalent scales, ΔT for Celcius is going to be the same in Kelvin.

Since the heat of reaction is an extensive property, it is dependent on the mass of the substance. This is why mass is included in this heat transfer equation.

Specific Heat

As you can see, the measurement of heat changes involves knowing specific heat, the amount of heat required to raise the temperature of a gram of a substance by 1° C. This can be used to determine heat capacity, the amount of heat required to raise the temperature of an object by 1° C.

Well...specific heat is the amount of energy required to raise the temperature of a gram of a substance by 1° C, but what the heck does this actually mean?

💧Water

Let's take a look at a real-life example: boiling water. Do you ever get annoyed at the speed at which water boils? It's soooo slow, it becomes annoying to wait when hungry.

The reason why water takes a long time to boil is because of its high specific heat. This means that water takes a long time to take in energy, or enough energy, for the water to boil. The specific heat of water is 4.184 J/g.

🏖️Sand

Now let's take a look at sand: does it heat up faster than water? When you go to the beach, you probably feel the scorching hot sand at your feet. It heats up a lot faster than water—it takes much less energy to heat sand up than it takes to heat water up. The specific heat of sand is about 0.840 J/g.

The specific heat of sand is much less than the specific heat of water. Therefore, we can conclude that the higher the specific heat, the more energy⚡ it takes for an object to heat up and cool down.

Usually, the specific heat of an object is given on the AP Chemistry exam. You just have to know when to plug it in (q=mCΔT is only one of the few equations in this unit😉).

Calorimetry Examples

Question 1

An insulated cup contains 255.0 grams of water and the temperature changes from 25.2 °C to 90.5 °C. Calculate the amount of heat released by the system. The specific heat capacity of water is 4.184 J/g°C.

When looking at this question, you should recognize that calorimetry is being used. Therefore, use q = mcΔT and plug in the values you know:

q = (255.0 g)(4.184 J/g°C)(90.5-25.2°C)

Make sure the units that you are using match since mass can be given in grams or kilograms. As long as the units of your mass match your specific heat, you should be good to go! For example, if you were to use 0.2550 kg and 4.184 J/g°C, you are mixing kilograms and grams, messing up your calculation. Let's solve the rest:

q = (255.0 g)(4.184 J/g°C)(65.3°C)

q = 69,700 J or 69.7 kJ since there are 1000 J in 1 kJ.

We will be going over more equations later in this unit, so whenever you see a temperature change in a problem, think about using this specific formula.

Misconception - q vs. ΔH

Right now, we can look at q and ΔH and think about heat. However, q does not equal ΔH.

For the purpose of this course, q is always going to be positive. You can think of it as a magnitude of energy. ΔH could be positive or negative though; it depends on if the heat is released or absorbed.

Question 2

The following question is from the Advanced Placement YT Channel. The following laboratory procedure is being done in a calorimeter.

Mass of Copper	50.00g
Initial Temperature of Copper	100.0°C
Mass of Water	100.00g
Initial Temperature of Water	20.0°C
Final Temperature of System (Copper and Water)	23.6°C
Specific heat capacity of water	4.18 J/g°C
Specific heat capacity of copper	?

(a) What is |ΔT| for the copper? What is |ΔT| for the water?

Whenever you see changes in temperature, you should automatically find the change in temperature (ΔT). ΔT is always calculated by final temperature - initial temperature.

Copper: |23.6°C - 100.0°C| = 76.4°C
Water: 23.6°C - 20°C = 3.6°C

(b) A student claims that, since the magnitude of ΔT for the copper is greater than that of the water, it means that the magnitude of heat (q) lost by the copper is greater than the magnitude of heat (q) gained by the water. Do you agree with this claim?

Let's recall the first law of thermodynamics: no energy could be created or destroyed. Therefore, the heat lost by the copper must be equal to the heat gained by the water.

Sample Response: Assuming the calorimeter lost no heat to its surroundings, the heat lost by the copper must equal the heat gained by the water, despite their significant changes in temperature.

(c) Find the specific heat of copper.

Considering we only learned one formula so far, we must use q=mcΔT. In general, however, if you see specific heat, the formula you have to use is most likely this one.

Since we are solving for c, we must be given q, the mass of the copper, and the change in temperature. One problem: we don't have q! Let's go back to part b...the magnitude of heat lost by the copper is equal to the magnitude of heat gained by the water.

This enables us to use q=mcΔT twice, by setting the water calculation equal to the copper calculation (q for copper is equal to q for water so what q equals for copper must be equivalent to what q equals for water).

The setup looks like this:

mcΔT (copper) = mcΔT (water)

(50.00 g)(C)(76.4 °C) = (100.00 g)(4.18 J/g°C)(3.6 °C)

C = 0.39 J/g°C

Another Formula

So we know that we could use q=mcΔT, but when we have a heat loss and heat gain question, we could also use:

heat loss = heat gain or mcΔT (1st substance) = mcΔT (2nd substance) like we just did!

Browse Study Guides By Unit

⚛️Unit 1 – Atomic Structure & Properties

🤓Unit 2 – Molecular & Ionic Bonding

🌀Unit 3 – Intermolecular Forces & Properties

🧪Unit 4 – Chemical Reactions