📚

All Subjects

🧪

AP Chem

🔥

Unit 6

6.9 Hess’s Law

5 min read•june 18, 2024

Anika P

Dalia Savy

AP Chemistry 🧪

269 resources

See Units

State Functions

In thermodynamics, we study changes in the state of a system. There are several terms you should be familiar with that will tie into Hess's Law, the focus of this study guide!

Pathway Dependent

A pathway is a route that a process takes. Typically, pathway dependency or independency is applied to functions. Essentially, if the result of something depends on the order in which you did it, it is pathway-dependent and if it is not, it is pathway independent.

In other words, pathway dependent refers to a process or system that requires a specific pathway or sequence of steps to function or operate. It is dependent on a particular pathway or sequence of events.

Pathway Independent

On the other hand, pathway independent refers to a process or system that does not require a specific pathway or sequence of steps to function or operate. It is not dependent on any particular pathway or sequence of events.

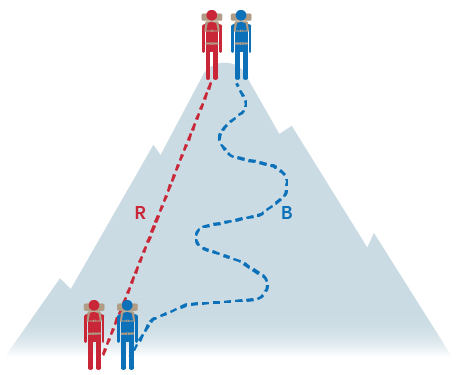
For example, the change in elevation of a mountain climber is pathway independent. You could walk in a straight line or a zig-zagged line up the mountain but regardless, you both end up at the top of the mountain. ⛰️

Remember state functions? Since only the initial and final states of the system are important, state functions are pathway independent. These include energy, enthalpy, pressure, volume, and temperature.

Hess's Law

Hess's Law is stated as simply as enthalpy is a state function. No matter what way you go from reactants to products, you will end up with the same enthalpy of reaction for the reaction. This means that if we know the enthalpy of formation for different reactions, we can manipulate them to get a single reaction and find the enthalpy of that single reaction. It's like magic, and it's kinda fun! ✨

Rules of Hess's Law

When a reaction is reversed, the enthalpy change stays constant in magnitude but becomes reversed in mathematical sign (Flipping the reaction flips the sign of ΔH🔁).
If an equation is multiplied by n, ΔH has to also be multiplied by n.
When two (or more) reactions are added to obtain an overall reaction➕, the individual enthalpy changes of each reaction are added to obtain the net change of enthalpy of the overall reaction.

Hess's Law Example Problem

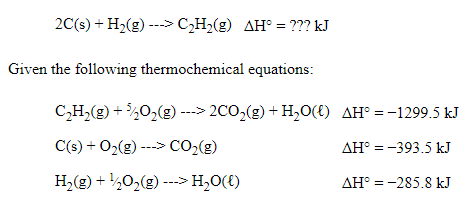
Our general strategy is going to be manipulating these three simple reactions and then adding them together to form the overall reaction. This is using Hess's Law to find the net enthalpy.

Thought Process

When I approach a Hess's Law question, I always find the reactants and products in the given thermochemical equations. This is what I would note🤔:

C (s) is a reactant in thermochemical equation #2 and in the overall equation, but there should be two atoms of carbon. Therefore, we have to manipulate the second equation and add a coefficient in front of the solid carbon. ❌
H₂ (g) is a reactant in thermochemical equation #3 and the overall equation, and the coefficient is 1 in both equations. Therefore, we do not have to manipulate the third equation. ✔️
C₂H₂ (g) is a reactant in thermochemical equation #1, but it is a product in the overall equation. This means we have to manipulate the first equation. ❌

Now that we have a general idea of what we are looking at, let's do the manipulations we know need to occur.

Steps to Take

Step 1: Flip reaction 1 to get C₂H₂ on the product side. If we flip the reaction, we also have to flip the sign on the enthalpy🔁. Our manipulated first equation is as follows: 2CO₂ (g) + H₂O (l) → C₂H₂ (g) + 5/2O₂ (g) with ΔH° = +1299.5 kJ

Step 2: Multiply reaction 2 to get 2 solid carbon atoms. If we multiply the reaction, we have to multiply the enthalpy by 2 too✖️.

Whatever you do to the equation, you have to do the same to the enthalpy.

Results of Steps

After doing these things, we are left with:

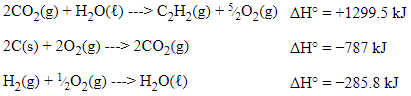
Now, the equations are set up properly to create the overall equation, but what happens with the extra compounds?

You could think of these as spectator compounds; they cancel out since they are present on both sides of the equation when all 3 equations are added together.

With this being said, the O₂s cancel out, H₂O cancels out, and the CO₂s cancel out.

👉 Since we added the reactions together, we can do the same with their enthalpies. This follows rule #3!

ΔH = +1299.5 kJ + (−787 kJ) + (−285.8 kJ) = +226.7 kJ.

Example Problem #2

Calculate the value of ΔHreaction for the following reaction using the listed thermochemical equations.

Thought Process

Let's note a few things🤔:

P₄O₁₀ is on the wrong side of the equation, so we have to manipulate equation 2. ❌
PCl₅ is also on the wrong side of the equation and it doesn't have a coefficient of 6, so we have to manipulate equation 3.❌
Cl₃PO is on the right side of the equation, but it doesn't have a coefficient of 10 so we have to manipulate equation 4. ❌

Steps to Take

This problem has a lot more steps! Let's go through the manipulations we have to make:

Step 1: Flip equation 2 to get P₄O₁₀ on the other side. If we flip the equation, we also have to flip the sign on the enthalpy🔁.

Step 2: Flip equation 3 to get PCl₅ on the other side and multiply equation 3 by 6 so PCl₅ has a coefficient of 6. In doing this, we have to multiply the enthalpy by 6 and negate it (two steps in one!)✖️🔁.

Step 3: Multiply equation 4 by 10 so that Cl₃PO has a coefficient of 10. In doing this, we also have to multiply the enthalpy by 10✖️.

Results of Steps

After doing these things, we are left with:

Now, we have everything on the right side of the equation, and they all have the proper coefficients. Our last step is to check if all the spectators cancel out, so let's count them up!

Compound	Reactant Side	Product Side	Is Manipulation Necessary?
P₄	1/4	1	✔️
Cl₂	3/2	6	✔️
PCl₃	10	7	✔️
O₂	5	5	❌

Luckily, all 3 compounds that we have to balance are in equation 1, meaning we now have to manipulate it in order for the equations to add up to the overall equation.

🤔What should we multiply equation 1 by? In order to get the same amount of each compound, we have to multiply equation 1 by 4 and its enthalpy by 4!