7.6 Properties of the Equilibrium Constant
6 min read•june 18, 2024
Dalia Savy
Dylan Black
AP Chemistry 🧪
269 resourcesSee Units
In Unit 6, we discussed Hess’s Law and how it can be used to find the value of ΔH for reactions by adding together, flipping, and multiplying reactions. In this section, we’ll apply similar rules to equilibrium! If you did well with Hess’s Law problems then you should do fine with problems involving the properties of the equilibrium constant.
Review of Hess's Law
Let's bring Hess's Law back into memory a little bit, as it'll help you with the content in this study guide. Hess's Law is stated as simply as enthalpy is a state function. No matter what way you go from reactants to products, you will end up with the same enthalpy of reaction for the reaction. This means that if we know the enthalpy of formation for different reactions, we can manipulate them to get a single reaction and find the enthalpy of that single reaction.
There are three major rules of Hess's Law:
- When a reaction is reversed, the enthalpy change stays constant in magnitude but becomes reversed in mathematical sign (Flipping the reaction flips the sign of ΔH🔁).
- If an equation is multiplied by n, ΔH has to also be multiplied by n.
- When two (or more) reactions are added to obtain an overall reaction➕, the individual enthalpy changes of each reaction are added to obtain the net change of enthalpy of the overall reaction.
Now, let's see how these rules can be applied to the equilibrium constant and its properties.
Properties of Keq
Flipping Reactions
Flipping reactions is essentially the equivalent of saying, “Let’s start with the products and end with the reactants”. Because of this, we can find out what our equilibrium constant will be by writing out the formula for the equilibrium constant for both equations:
If our original reaction was A ⇌ B, that would make K = [B]/[A]. Let’s think about our K value for the reverse, B ⇌ A. You may think that the equilibrium constant would be the same because A ⇌ B is reversible, but in this case the forward reaction is what the backward reaction really is. You're basically changing your perspective when looking at the chemical equation. Rewriting our equilibrium formula for B ⇌ A we find that K₂ = [A]/[B] = 1/K.
From here we can conclude that flipping a reaction gives it a new K value of 1/K.
Example of Inverting K
Let’s look at the following example and how flipping a reaction quantitatively alters Keq.
Consider the reaction N₂ + 3H₂ ⇌ 2NH₃ that has a K = 0.118. Find the equilibrium constant for the reaction 2NH₃ ⇌ N₂ + 3H₂.
Once you recognize that the new reaction is the reverse of the initial reaction, you can easily find K for 2NH₃ ⇌ N₂ + 3H₂ to be 1/0.118 = 8.47. Think of this as Final K = 1/Initial K.
Fun Fact! This reaction has a special name called the Haber Process and is useful for creating fertilizers among many other useful chemicals!
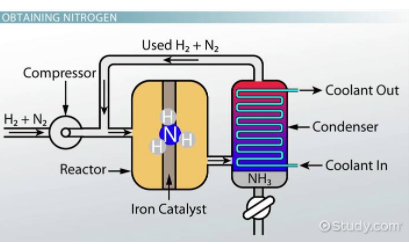
Image Courtesy of Study.com
Multiplying Reactions
Let’s take a look at what happens when we multiply a reaction by a coefficient. When we say multiplying a reaction, we mean taking something like A ⇌ B and multiplying it by a constant n to form nA ⇌ nB.
If n=2, our new chemical equation would be 2A ⇌ 2B. This does not change the reaction besides the number of moles that go in and out (the equation remains balanced either way!), but it does change the equilibrium constant. Let’s explore why:
For the reaction A ⇌ B, K = [B]/[A]. We established this same fact in part 1.
However, for the reaction 2A ⇌ 2B, K = [B]² / [A]² = ([B]/[A])² = K².
Let’s see if we can generalize this to any n coefficient:
For the general multiplied reaction nA ⇌ nB, K = [B]ⁿ / [A]ⁿ = ([B]/[A])ⁿ = Kⁿ.
What does this tell us about how multiplying a reaction impacts the equilibrium constant? It tells us that when we multiply a reaction, our K value gets exponentiated that same amount. For example, multiplying a reaction by 3 cubes K.
Example of Exponentiating K
Let’s take a look at a real example:
Like before, Consider the reaction N₂ + 3H₂ ⇌ 2NH₃ that has a K = 0.118. Find the equilibrium constant for the reaction (1/2)N₂ + (3/2)H₂ ⇌ NH₃.
Comparing the two reactions, you'll quickly notice that only the stoichiometric coefficients have changed, but to what degree? In this case, we've multiplied our reaction by ½. This means that our original K value, 0.118, is raised to the ½ power.
K = (0.118)¹/² = 0.343.
Adding Reactions Together
The crux of this section is what happens when we learn what happens when reactions are added together. Like before, let’s look at a general example without any real chemicals:
A ⇌ B : K = [B]/[A]
C ⇌ D : K = [D]/[C]
A + C ⇌ B + D : K = [B][D] / [A][C].
What does this mean? We have two reactions, A ⇌ B and C ⇌ D that we’re adding together to form A + C ⇌ B + D. However, take a look at what happens to our equilibrium constants. It may seem like nothing happened, but in fact, in adding the reactions together we actually multiplied our equilibrium constants! K1 was [B]/[A] and K2 was [D]/[C] which multiplied to form [B][D] / [A][C]! Therefore, when we add reactions together we multiply the K values together.
Summary of Properties of K
We’ve covered 3 main rules that you may have to combine in problems. Here’s a table of the rules we’ve learned so far and a side-by-side comparison to Hess's Law.
Practice Problem
Using the following 2 reactions, find the equilibrium constant for the reaction N₂ + 2O₂ ⇌ 2NO₂.
- Reaction 1: (1/2)N₂ + (1/2)O₂ ⇌ NO …. K₁ = 6.55 * 10⁻¹³
- Reaction 2: 2NO + O₂ ⇌ 2NO₂ …. K₂ = 6.9 * 10⁵
We have two reactions that sorta look like the reaction we want, so let’s think about ways to get these reactions into a form that allows us to form our reaction by adding the two up.
If we multiply reaction 1 by the constant 2, we’ll get N₂ + O₂ ⇌ 2NO and the subsequent K value of (6.55 * 10⁻¹³)² = 4.3 * 10⁻²⁵.
Next, adding together our multiplied reaction 1 with reaction 2, we’ll find that they equal the reaction that we want! The NOs will cancel out, the (1/2)N₂ is now N₂, and our O₂s will add to form 2O₂. Therefore, our final K will be 4.3 * 10⁻²⁵ * 6.9 * 10⁵ = 3.0 * 10⁻¹⁹.
You may be wondering how to know what to do when you’re given one of these problems without any clear steps. There really is no rhyme or reason, you just have to follow the three rules in a way that makes sense to you.
Browse Study Guides By Unit
⚛️Unit 1 – Atomic Structure & Properties
🤓Unit 2 – Molecular & Ionic Bonding
🌀Unit 3 – Intermolecular Forces & Properties
🧪Unit 4 – Chemical Reactions
👟Unit 5 – Kinetics
🔥Unit 6 – Thermodynamics
⚖️Unit 7 – Equilibrium
🍊Unit 8 – Acids & Bases
🔋Unit 9 – Applications of Thermodynamics
🧐Exam Skills
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.