Peter Apps
AP Physics 1 🎡
257 resourcesSee Units
The Paragraph-Length Response is one of the 5 FRQs that appear on the AP Physics 1 Exam. This particular question is usually worth 7 points (out of a total of 45) and is suggested to take around 13 minutes to complete.
What is the Reader Looking for?
From CollegeBoard:
AP Physics students are asked to give a paragraph-length response so that they may demonstrate
their ability to communicate their understanding of a physical situation in a reasoned, expository
analysis. A student’s response should be a coherent, organized, and sequential description of the
analysis of a situation. The response should argue from evidence, cite physical principles, and
clearly present the student’s thinking to the reader. The presentation should not include
extraneous information. It should make sense on the first reading.
How do I do it?
So we need to have a logical, organized argument that describes a situation from given evidence and basic physics principles. To do that I recommend using the following Claim, Evidence, Reasoning (CER) format:

Image Courtesy of mtlsd.net
With this format in mind, let's apply it to a sample problem.
Sample Problem #1
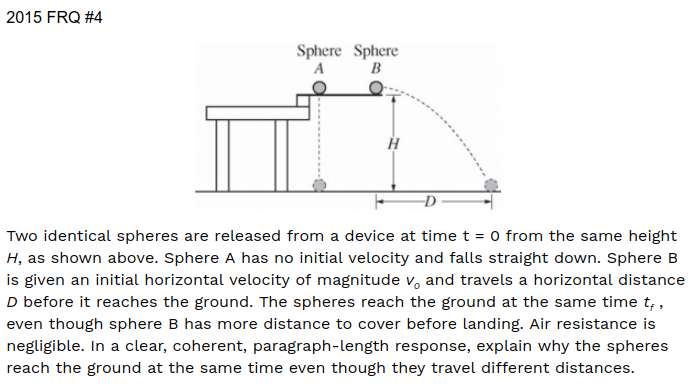
Claim - We're told in the question that we need to explain why the spheres take the same amount of time to hit the ground, so our claim is already done for us.
Evidence - There are several things that we could use as evidence for this claim. It might be tempting to just start writing this out, but remember we need it to be logical. Let's start with the basic physics principles here:
- Both objects are in freefall (the only force acting on them is the force of gravity)
- Vertical and Horizontal motion are independent of each other
- Possible useful equation(s) from the reference table (Kinematics & Forces):
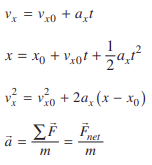
Reasoning - Hopefully at this point, we can start to see a plan coming together:
- Same Forces & Masses --> Same Vertical Acceleration
- Same Height, Starting Vertical Velocity, and Vertical Acceleration --> Same time to fall
- Rewriting equation #2 and solving for time might be useful too
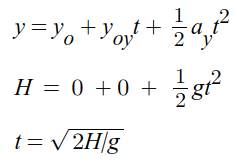
Answer - Putting it all together, one possible response could be:
The spheres will hit the ground at the same time because their vertical motion is independent of their horizontal motion. The time to fall can be calculated using y = yo + voyt + 1/2at^2. The spheres both start with the same vertical initial velocities, acceleration (g), and distance above the ground. This lets us simplify the equation to t = sqrt(2h/g) which is identical for both spheres. Therefore the spheres will hit the ground at the same time even though one of the spheres has an initial horizontal velocity and travels a greater distance.
Sample Problem #2
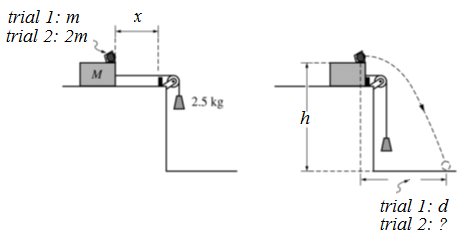
Image Courtesy of jacobsphysics.blogspot.com
A ball of mass m is in a cup of negligible mass attached to a block of mass M that is on a table. A string passing over a light pulley connects the blocks to a 2.5 kg object, as shown above. The cup is a vertical distance h off of the floor. All friction is negligible. In Trial 1, the system is released from rest, the block accelerates to the right, and after moving a distance x the block collides with a bumper near the end of the table. The ball continues to move and lands on the floor at a position a distance d horizontally from where it leaves the cup. In Trial 2, the mass m of the ball in the cup is doubled. The system is again released from rest. The block collides with the same bumper, the ball continues to move, and lands on the floor. In trial 2, does the heavier ball land a horizontal distance from the table that is greater than, less than, or equal to d? Justify your answer in a clear, coherent, paragraph-length explanation.
Claim - This time we're given three choices for our claim: greater than d, less than d, or equal to d. If you're not certain yet, we can always come back to this part after we've looked at the evidence
Evidence -
Principles
- Falling mass provides the net force to the system (F = ma)
- Mass M and ball travel the same distance on the table (x) each trial
- Ball goes through projectile motion after it leaves the cup
- Horizontal distance depends on time in air and horizontal velocity
- Height and initial vertical velocity are the same in each trials
Reasoning -
Same net force, but more mass in trial 2 --> less acceleration for trial 2
Less acceleration, but same x --> less horizontal velocity for trial 2
Same vertical velocity, vertical acceleration and height for both trials --> same time in the air
Less horizontal velocity and same time --> less distance traveled in the air for trial 2
Conclusion - Trial 2's distance will be less than Trial 1's
Answer -

🎥Watch: AP Physics 1 - Paragraph-Length Responses
Browse Study Guides By Unit
👟Unit 1 – Kinematics
🌀Unit 2 – Dynamics
🚀Unit 3 – Circular Motion & Gravitation
⚡️Unit 4 – Energy
⛳️Unit 5 – Momentum
🎸Unit 6 – Simple Harmonic Motion
🎡Unit 7 – Torque & Rotational Motion
💡Unit 8 – Electric Charges & Electric Force
🔋Unit 9 – DC Circuits
🔊Unit 10 – Mechanical Waves & Sound
📚Study Tools
🧐Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.