Quantitative / Qualitative Translation
6 min read•june 18, 2024
Peter Apps
AP Physics 1 🎡
257 resourcesSee Units
The Qualitative / Quantitative Translation is one of the 5 FRQs that appear on the AP Physics 1 Exam. This particular question is usually worth 12 points (out of a total of 45) and is suggested to take around 25 minutes to complete. The word qualitative implies the use of words. The word quantitative implies the use of mathematics. This means that a QQT is a question that requires you to go between words and mathematics in describing and analyzing a situation.
What you might be asked to do on a QQT
Work with multiple representations - You may be given one representation of a situation and asked to create another representation of the same situation. Representations can include math equations, word descriptions, graphs, diagrams, and data tables.
Evaluate a student’s words - You will be presented with a situation, a question, and one or two students’
answers or arguments over what the answer is. You will be asked to break down their reasoning, identifying
each feature that is correct or incorrect. Sometimes you will have to connect the correct (or incorrect) features
of arguments to physics principles or equations. After figuring out what is right and wrong, you may be
asked to construct a completely correct argument based on the “rights” and “wrongs” you found.
Evaluate a student’s representations - You may be shown a student’s graph or work that describes the situation, but there may be features of the graph or equation that are wrong. You will need to identify the correct or incorrect features of the graph. You may be asked to then create a correct version of their representation.
What to look for:
Things to look for when evaluating a graph:
- Does it have a slope (positive/negative/zero) that makes sense?
- Ex. An object that is moving in the positive direction and speeding up should have a positive slope
- Does it have an intercept (on the y-axis or x-axis or none at all) that makes sense?
- Ex. A Period vs Length graph for a pendulum should have a 0,0 intercept.
- Ex. A velocity vs time graph should have a y-intercept equal to the initial velocity
- Should the graph be a line or a curve?
- Is the relationship linear (Fs = kx) or quadratic (Us = 1/2kx^2)?
Things to look for when evaluating equations:
- The symbols in the numerator - when they increase, does the quantity of interest increase?
- The symbols in the denominator - when they increase, does the quantity of interest decrease?
- Should a variable be inversely (one decreases if another increases, y=k/x) or directly related (one increases if another increases, y=1/2ax^2)?
Things to look for when evaluating a student’s words:
- If the student uses proportional reasoning (sounds like this: “if the speed of a car doubles, then it has twice the energy”) check the equation that shows this relationship (in this case, K = 1/2mv^2) and see if there is actually a direct relationship (in this case, no it's a quadratic relationship). You would need to correct the student on this (it's actually four times the energy).
- If the student says that something increases or decreases (sounds like this: “if the ball moves faster, then the time it takes to pass through the photogate increases”), check to see if that makes sense (“no it doesn’t—a faster ball would spend less time passing through a photogate). Get ready to correct the student’s wrong reasoning.
Sample Problem #1
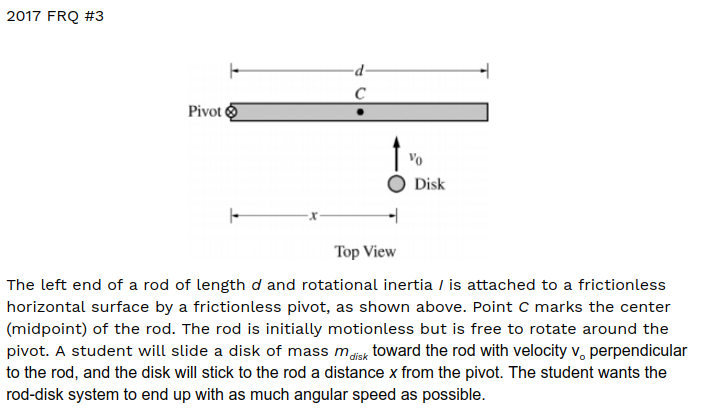

The student should aim to the right of point C. In order to change the angular speed of the rod, a torque needs to be applied to it. The amount of torque depends on the force and the distance from the pivot. Increasing the distance from the pivot increases the torque which will increase the angular speed.

This equation agrees with my reasoning in part (a). If the distance from the pivot (x) is increased the angular speed 𝜔 increases as well.
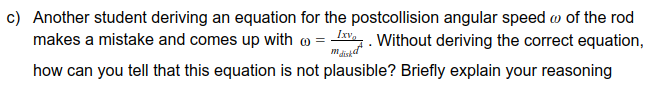
This equation shows that increasing the mass of the disk would result in a slower angular speed because mdisk is in the denominator. But a more massive disk has more angular momentum to transfer to the rod and should result in a larger angular speed. Also, a larger moment of inertia I makes the rod more difficult to rotate and should give a smaller angular speed not a larger one, so I should be in the denominator not the numerator.

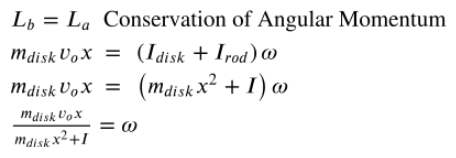

The disk bouncing off the rod has a larger change in angular momentum than when it sticks to the rod. This results in a larger angular speed in the rod afterwards because the total angular momentum of the rod-disk system has to remain constant.
Sample Problem #2
(From National Math + Science Initiative)
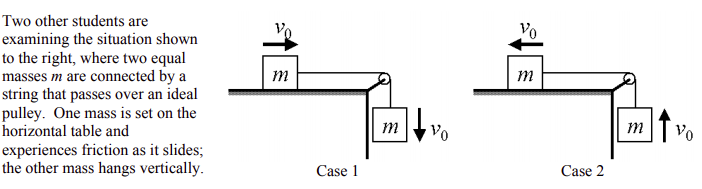
Two cases are shown:
Case 1 in which the block on the table is initially moving to the right, and Case 2 in which the block on the table is initially moving to the left. The two students are arguing over which case has greater acceleration and which case has greater tension in the string.
Student X: “Both cases have the same hanging mass, so both cases have the same net force on the two-block
system. Both cases have the same mass on the table, so both cases have the same frictional force on the table block. If both cases have the same forces and the same masses, they must have the same accelerations and the same tensions.”
Student Y: “But you are not taking into account the direction of the friction force. In Case 1, the friction and
hanging weight forces work together to create a greater net force than in Case 2. A greater net force means a greater acceleration in Case 1. If the acceleration is greater, then the tension pulling the block on the table must be greater in Case 1 as well.”
i. Which aspects of Student X’s reasoning are correct? Explain why they are correct.
Student X correctly states that both cases have the same hanging mass (shown in diagram), same force of friction on the table (Same mass on the table and same coefficient of friction, so Ff = 𝜇Fn will be the same)
ii. Which aspects of Student X’s reasoning are incorrect? Explain why they are wrong.
The forces between the 2 trials are not the same. In case 1 the frictional force and the weight of the hanging block are in the same direction (right / down) and result in a larger net force. This leads to a larger acceleration for case 1. The tension on the string in case 1 is smaller, since the acceleration is greater for the hanging block (mg-T=ma) In case 2, the frictional force is to the left and is opposing the weight of the hanging block, which gives a smaller net force and acceleration. The tension is greater in case 2 as well.
iii. Which aspects of Student Y’s reasoning are correct? Explain why they are correct.
Student Y correctly states that the frictional force changes direction (opposes the motion of the blocks) which gives a greater net force & acceleration in Case 1 (see reasoning in part ii for more detailed explanation)
iv. Which aspects of Student Y’s reasoning are incorrect? Explain why they are wrong
Greater acceleration doesn't mean greater tension in the cord. In fact the opposite is true. Looking just at the hanging block, we can derive a Newton's 2nd Law equation to show this.
F = ma
mg - T = ma
T = mg - ma <-- a larger acceleration means a smaller tension!
Browse Study Guides By Unit
👟Unit 1 – Kinematics
🌀Unit 2 – Dynamics
🚀Unit 3 – Circular Motion & Gravitation
⚡️Unit 4 – Energy
⛳️Unit 5 – Momentum
🎸Unit 6 – Simple Harmonic Motion
🎡Unit 7 – Torque & Rotational Motion
💡Unit 8 – Electric Charges & Electric Force
🔋Unit 9 – DC Circuits
🔊Unit 10 – Mechanical Waves & Sound
📚Study Tools
🧐Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.