📚

All Subjects

🧲

AP Physics 2

⚛️

Unit 7

7.6 Photoelectric Effect

6 min read•june 18, 2024

Saarah Hasan

Daniella Garcia-Loos

AP Physics 2 🧲

61 resources

See Units

Photoelectric Effect

The idea that light exhibits particle properties was first suggested by Einstein when he showed that light transferred energy just like a particle(E=mc^2). Compton expanded the groundwork of this idea further in 1923 when he showed that light has momentum and can undergo elastic collisions. From multiple physicists' work, we now know that light behaves like a stream of photons, which can be illustrated by the photoelectric effect:

The photoelectric effect is the phenomenon in which electrons are emitted from a metal surface when it is exposed to light.

Here are some key points about the photoelectric effect at an AP Physics level:

The photoelectric effect is the phenomenon in which electrons are emitted from a metal surface when it is exposed to light. It is an important concept in physics and is used to understand the behavior of electrons in materials and to predict the behavior of physical phenomena.
The photoelectric effect occurs when light of a high enough frequency is shone on a metal surface. The light causes the electrons in the metal to be excited and to be emitted from the surface.
The energy of the emitted electrons is dependent on the frequency of the light, but not on the intensity of the light. This is known as the Einstein relationship.
The photoelectric effect is an important concept in quantum mechanics and is used to understand the behavior of electrons in materials and to predict the behavior of physical phenomena. It is also used in a variety of applications, including solar cells, detectors, and lasers.

When light shines on a piece of metal, some of the photons enter the surface of the metal, collide with the atoms and get absorbed, giving energy to the metal’s surface electrons. If this energy is great enough, the electrons can jump from their bound state and fly off. These electrons that break free are known as photo-electrons.

Taken from Wikimedia Commons

There would be a large time delay between the point when the light shined on the metal and when the electrons would break off.
Increasing the intensity of light would cause the photo-electrons to be ejected with greater kinetic energy, since a wave’s energy is related to its intensity.
All frequencies of light would cause photoelectrons to eject, as long as the intensity was high enough.

What actually happened:

Electrons broke off within a few billionths of a second after getting shined on.
Increasing the intensity of light didn’t increase the photoelectron’s kinetic energy. More electrons flew off as the intensity increased, but there was a certain maximum photoelectron kinetic energy.
For each metal, there was a specific threshold frequency, f0. If the light’s frequency was lower than the f0, then no electrons flew off. The intensity of the light wasn’t a factor.

The energy of a photon can be found by:

E=hf

where h = Planck’s constant = 6.63 ∗ 10^−34 J*s

f = frequency

Remember that:

f=c/λ

E=hf➡️

E=hc/λ

In order for the metal’s surface electrons to break free, a certain amount of energy has to be transferred to them. This is known as the metal’s work function(Φ). If an electron absorbed a photon with an energy (E) greater than Φ, then it would eject with a maximum kinetic energy of: K(max)=E-Φ ➡️ Kmax= hf-Φ

The threshold frequency can be expressed as: f_0=Φ/h

Some things to keep in mind:

The kinetic energy of the photoelectrons is independent of the intensity of light.

The greater the light’s intensity, the more electrons ejected, hence the current increases.

Practice Problems: 🧩

1. Light of a single frequency falls on a photoelectric material but no electrons are emitted. Electrons may be emitted if the A) frequency of light is decreased

B) frequency of light is increased

C) intensity of light is decreased

D) intensity of light is increased

E) velocity of light is increased

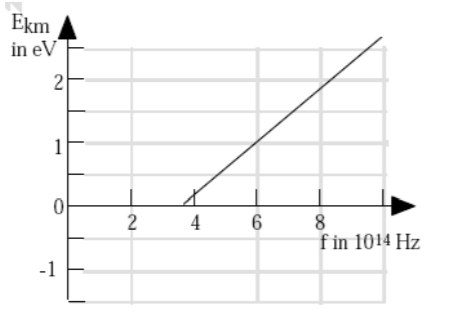
2. A student performs the photoelectric effect experiment and obtains the data depicted in the accompanying graph of Ekm (max kinetic energy) of photo-electrons vs the frequency of the photons. What is the approximate work function of this material?

A) 1.5 eV

B) 2.0 eV

C) 2.7 eV

D) 4.0 eV

E) 6.0 eV

3. Which graph best shows the maximum kinetic energy K of the photoelectrons as a function of the frequency of incident light? A) A

B) B

C) C

D) D

E) E

4. Which graph best shows the maximum kinetic energy K of a photo-electron as a function of the intensity of incident light? A) A

B) B

C) C

D) D

E) E

5. In the photoelectric effect, the maximum speed of the electrons emitted by a metal surface when it is illuminated by light depends on which of the following? I. Intensity of the light II. Frequency of the light III. Nature of the photoelectric surface A) I only

B) III only

C) I and II only

D) II and III only

E) I, II, and III

Answers:

B: Standard photoelectric effect question. If the frequency does not cause emission, it is below the threshold and will not be able to cause emission. The only way to cause emission is the increase the frequency above the threshold.
A: From K = hf – ϕ … y = mx + b … the work function is the y-intercept, extend the line
A: Below a threshold frequency, there would be no emissions and thus zero K for everything below that point. Above that threshold, more frequency means more K based on K = hf – ϕ, with h as the constant slope. Graph A has all these properties.
E: Intensity has no effect on the energy of a single given photo-electron. Each photo-electron’s energy is simply based on K = hf – ϕ. More intensity means a larger total number of photo-electrons and would result in more total energy, but the energy of each photo-electron is the same for all levels of the overall intensity.
D: Intensity has no effect on the energy of a single given photo-electron. Each photo-electron’s energy is simply based on K = hf – ϕ. More intensity means a larger total number of photo-electrons and would result in more total energy, but the energy of each photo-electron is the same for all levels of the overall intensity. K is based on the work function (which is based on the nature of the surface) and K is also based on the frequency of the incoming light.
B: The K of each photo-electron is given by. K = hf – ϕ. To reduce the energy of each photon, we need less f (which means more λ) for the incoming light. Since intensity is directly related to the number of photo-electrons emitted we want to increase the intensity.