7.7 Wave Functions and Probability
6 min read•june 18, 2024
Jed Quiaoit
AP Physics 2 🧲
61 resourcesSee Units
Probability: The Anatomy of a Wave Function
In quantum mechanics, the probabilistic description of matter is modeled by a wave function, which is a mathematical function that can be assigned to an object to describe its motion and interactions. The wave function is a complex-valued function that can vary in space and time, and it provides a complete description of a particle's quantum state. 🕰️

Source: Physics Travel Guide
The wave function of a particle is related to the probability of finding that particle in a given region of space. This is because the absolute value of the wave function squared gives the probability density of finding the particle at any given point in space. This relationship between the wave function and probability is one of the fundamental principles of quantum mechanics.
The wave function can be used to describe the motion of particles in various physical systems, including atoms, molecules, and solids. It can also be used to describe the interactions between particles, such as scattering and tunneling. The wave function provides a powerful tool for understanding the behavior of matter on a microscopic level and has led to many important discoveries in physics and chemistry.
Source: Quantum Journal
To analyze the wave function of a particle, one can use graphical methods to visualize the probability density distribution. For example, a probability density plot can be created to show the likelihood of finding a particle at any given point in space. While the probabilistic nature of quantum mechanics can be difficult to grasp intuitively, the wave function provides a powerful tool for understanding the behavior of matter on a microscopic level.
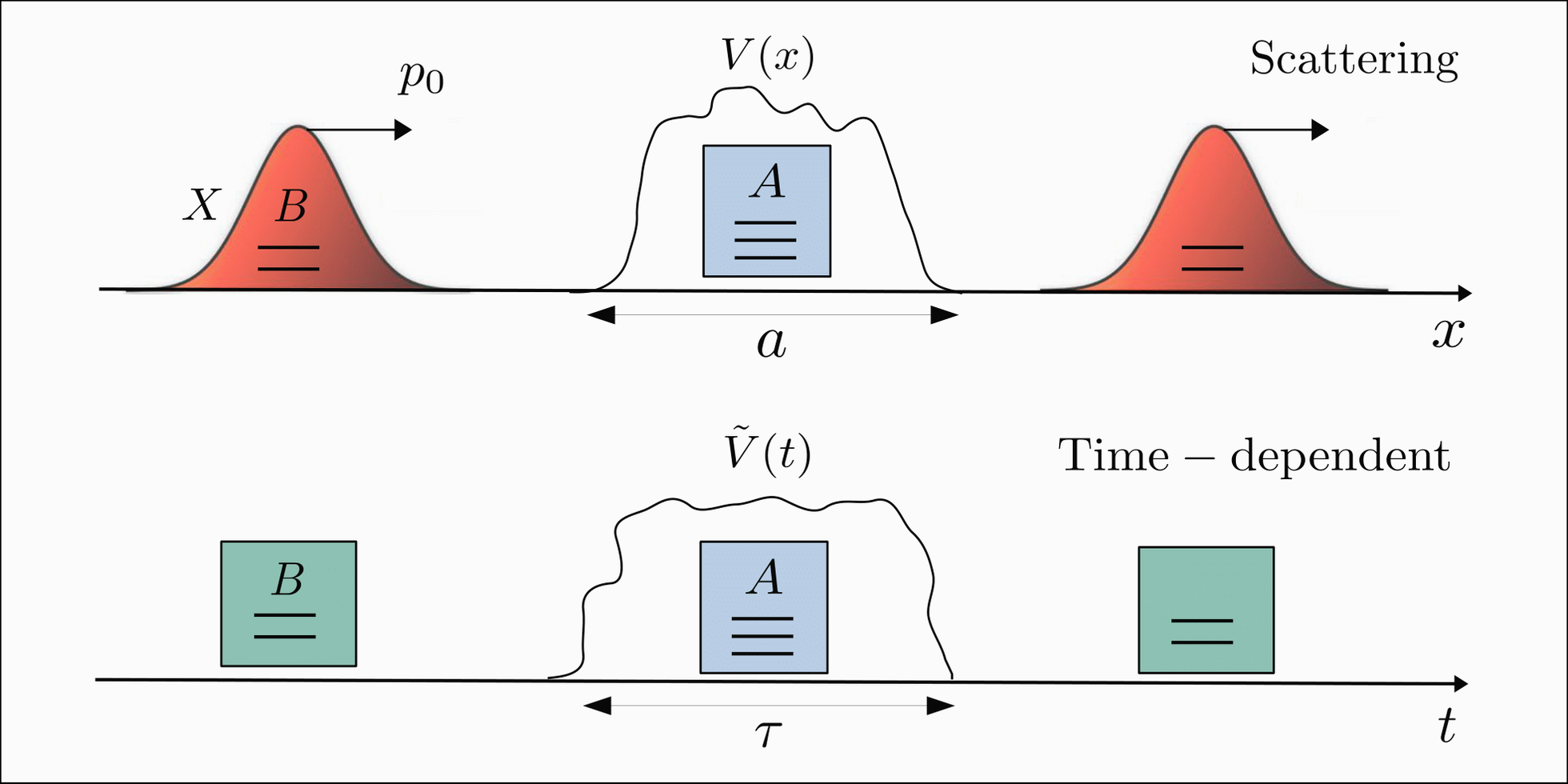
Allowed Electron Energy States
One of the most important implications of the wave model of an electron is that the allowed states for an electron in an atom can be calculated from the wave function. These allowed states are known as energy levels, and they represent the specific energies that an electron can have within an atom. ⚡
Source: Wondrium Daily
The energy levels of an electron in an atom are determined by the shape of the wave function and the boundary conditions that apply to the system. The wave function must satisfy certain conditions, such as being continuous and finite, and these conditions determine the possible energy levels that an electron can have.
The energy levels of an electron in an atom have important implications for the behavior of atoms and molecules. For example, the energy levels determine the spectra that are observed when atoms emit or absorb light. The energy levels also determine the chemical reactivity of atoms and molecules, as electrons in different energy levels can participate in chemical reactions in different ways.
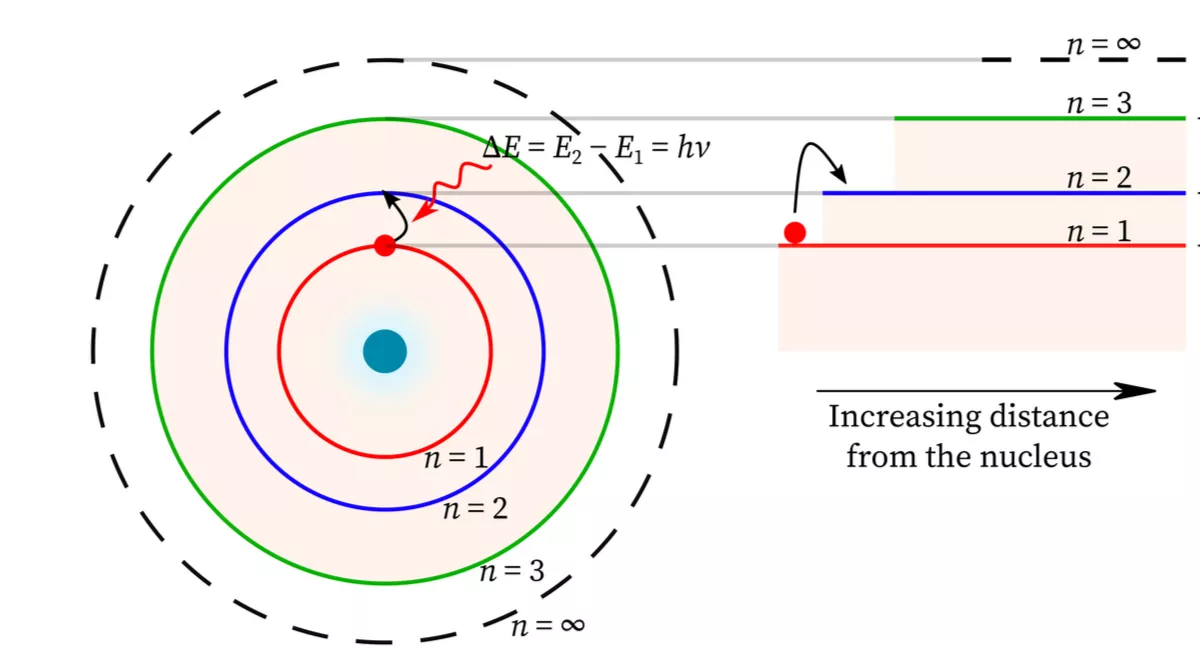
Standing Waves
The allowed energy states of an electron in an atom are modeled as standing waves, which are waves that do not appear to move or propagate but instead oscillate in place. These standing waves are described by a wave function, which contains all of the information about the electron's position, momentum, and energy. 🌊
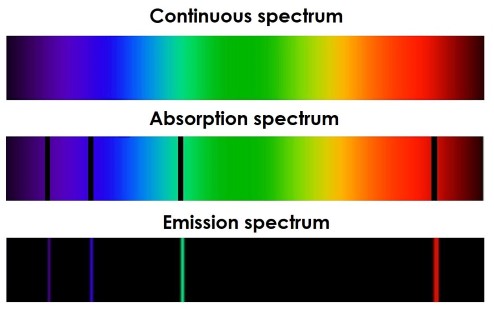
The standing wave model of electron energy levels has important implications for the behavior of atoms. When an electron moves from one energy level to another, it must absorb or emit energy in the form of a photon. This leads to the observation of discrete spectral lines in the emission and absorption spectra of atoms.
Source: The Star Garden
The spectral lines observed in the emission and absorption spectra of atoms are a direct result of the standing wave model of electron energy levels. The energy of each photon emitted or absorbed corresponds to the difference in energy between two energy levels. Because the energy levels are discrete and fixed, the energy of the emitted or absorbed photons is also discrete and fixed, leading to the observation of sharp, distinct spectral lines.
The study of spectral lines has been an important tool for understanding the behavior of matter on a microscopic level. It has allowed researchers to identify the chemical elements present in stars and other astronomical objects, and has provided important insights into the structure of atoms and the behavior of electrons.
de Broglie Wavelength
The de Broglie wavelength is a concept in quantum mechanics that relates the momentum of a particle to its wave-like behavior. Specifically, the de Broglie wavelength of an electron can be calculated by dividing Planck's constant by the electron's momentum. This wavelength can then be used to model the behavior of the electron in different situations. 📏
One important application of the de Broglie wavelength is in understanding the discrete transitions that occur between energy states in an atom. According to the standing wave model of electron energy levels, the allowed states for an electron in an atom are represented as standing waves with fixed energies. When an electron transitions from one energy level to another, it emits or absorbs a photon with an energy equal to the difference between the two energy levels.

Source: Quora
By using the de Broglie wavelength to model the electron as a wave, we can understand this process as a transition between standing waves. When an electron transitions from a higher energy level to a lower energy level, its wave function changes to match the new energy level.
This transition is accompanied by the emission of a photon with a wavelength that is related to the energy difference between the two levels. Similarly, when an electron absorbs a photon and transitions from a lower energy level to a higher energy level, its wave function changes to match the new energy level.
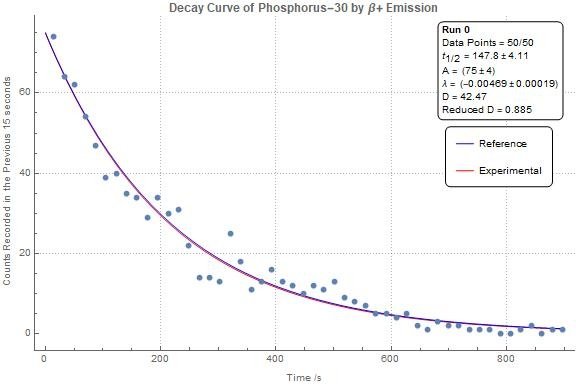
Probability: Radioactive Decay
The natural process of radioactive decay that occurs in individual nuclei is described by probability. This means that while we cannot predict when a specific nucleus will undergo a change, we can make predictions about what will happen on average to a large number of identical nuclei. ☢️
Source: Quora
Radioactive decay is characterized by the release of energy and a change in the nucleus. This process is related to the interplay between mass and energy, and results in the emission of kinetic energy or electromagnetic radiation.
One key measure of radioactive decay is the half-life, which is defined as the time it takes for half of a given number of radioactive nuclei to decay. Different unstable elements and isotopes have vastly different half-lives, ranging from fractions of a second to billions of years. For example, carbon-14 has a half-life of approximately 5,700 years, while uranium-238 has a half-life of 4.5 billion years.
Probability: Photon Emission & Absorption
Photon emission and absorption processes are fundamental to the interactions between matter and electromagnetic radiation. These processes are described by probability and are governed by the laws of quantum mechanics. 📸
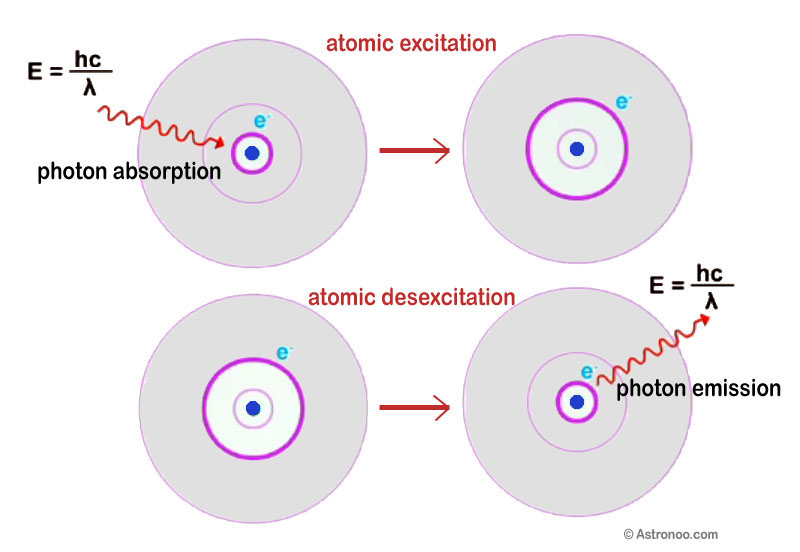
Source: Astronoo
An atom in a given energy state may absorb a photon of the appropriate energy, causing it to move to a higher energy state. This is known as stimulated absorption, which requires the atom to absorb a photon with precisely the correct energy level. The probability of this process occurring is determined by the properties of the atom and the characteristics of the incoming photon.
Conversely, an atom in an excited energy state may spontaneously transition to a lower energy state by emitting a photon. This process is known as spontaneous emission, and it occurs because the excited state is not stable, and the atom must release energy to return to its ground state. The probability of spontaneous emission depends on the energy of the excited state and the time that the atom spends in that state.
It is essential to note that spontaneous transitions to higher energy states have a very low probability, while transitions to lower energy states are highly probable. In rare instances, a spontaneous transition to a higher energy state can be stimulated to occur. However, this requires a high-intensity electromagnetic field and is not a common occurrence.
Stimulated emission occurs when a photon of the appropriate energy interacts with an atom in an excited state, causing it to transition to a lower energy state and emit a photon. In this process, both photons have the same energy, are in phase, and travel in the same direction. Stimulated emission is a crucial process in the functioning of lasers, which use this principle to produce coherent light. 🌈
Browse Study Guides By Unit
💧Unit 1 – Fluids
🔥Unit 2 – Thermodynamics
⚡️Unit 3 – Electric Force, Field, & Potential
💡Unit 4 – Electric Circuits
🧲Unit 5 – Magnetism & Electromagnetic Induction
🔍Unit 6 – Geometric & Physical Optics
⚛️Unit 7 – Quantum, Atomic, & Nuclear Physics
📆Big Reviews: Finals & Exam Prep
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.