3.2 Forces and Potential Energy 🎢
4 min read•december 24, 2021
AP Physics C: Mechanics ⚙️
68 resourcesSee Units
3.2: Forces and Potential Energy 🎢
Hooke's Law
Robert Hooke came up with an equation to describe an ideal "linear" spring acting in a system.
The equation for Hooke's Law is as follows:
Where Fs is the spring force, k is the spring constant, and Δ x is the displacement of the spring from its equilibrium position. Keep in mind spring force is a restoring force!
⚠️Hang on...what's a spring constant?
A spring constant is a number used to describe the properties of a spring, primarily its stiffness. Essentially, the easier a spring is to stretch, the smaller the spring constant is (start thinking about how this relates back to Newton's Third Law).
Many times, students will be asked to graph this relationship in order to find the spring constant k. Here's an example of a graph from a lab:
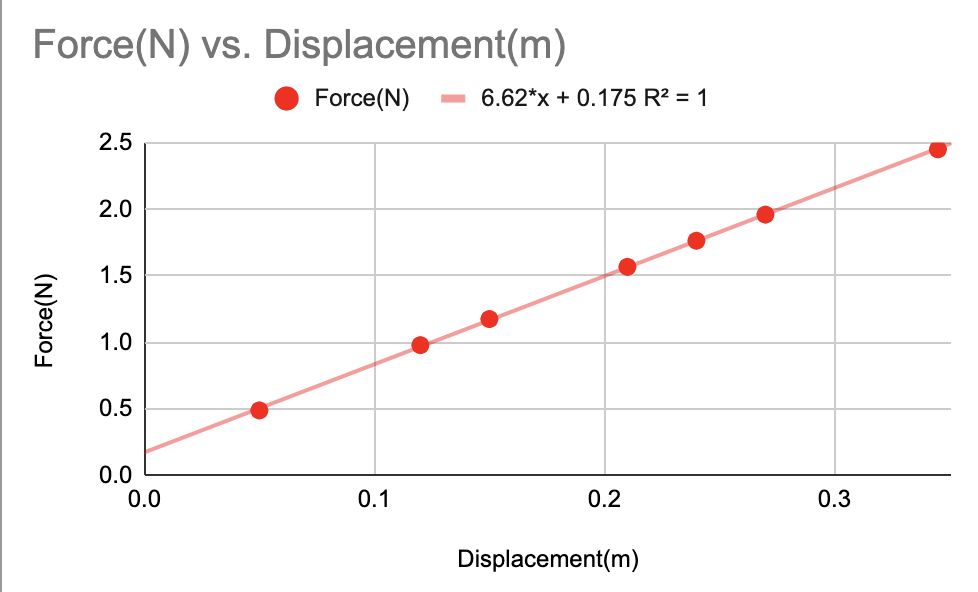
As you may be able to tell, the spring constant of the spring used in the lab should be the slope of the graph. (You can also see why this law describes "linear" springs)
Now let's connect this back to energy! The elastic potential energy of a spring can be defined as:
Conservative Forces
A conservative force is a force where the total work done on an object is solely dependent on the final and initial positions of the object. Dissipative forces are the opposite of conservative forces, and the ones typically seen are friction or external applied forces.
Fast facts of conservative forces:
- Independent of the path taken
- Total work on a closed path is zero
Examples of conservative forces:
- Gravitational force
- Spring force
Work done by conservative forces is also equal to the negative change in potential energy (U).
It can also be written as:
Where F is a conservative force and a and b are typically the the initial and final radius.
The differential version of this equation is:
We can do some fun things with this version of the equation, especially with graphs. The most important thing to note is that force is the negative slope of a potential energy versus position graph. AP loves to make students analyze energy graphs. Let's take a look at some examples!
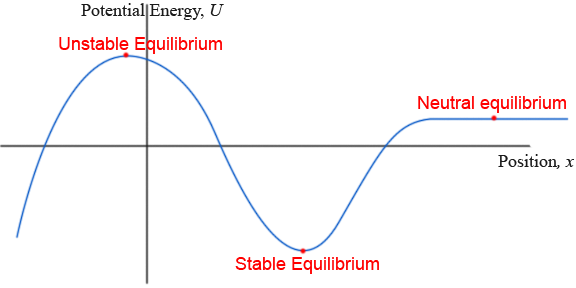
Taken from LibreTexts
From your expert calculus knowledge, you should be able to see that equilibrium is wherever the slope is zero, meaning there is no net force. When analyzing these graphs, you should attempt to determine the total mechanical energy and draw a horizontal line for it. Occasionally you will find graphs that contain a section known as Potential Energy Wells which are typically caused by oscillations. You can spot a potential energy well at a local minimum!
Gravitational Potential Energy
The gravitational potential energy of a system with an object very near/on the Earth in a uniform gravitational field is:
Where delta U is the change in potential energy, m is mass, g is acceleration due to gravity, and delta h is the change in height.
Here's the derivation for the equation for Gravitational Potential Energy (for large masses at a distance:
Where W is work, F(r) is a function for the force and r is the radius/distance.
Plug in the formula for Newton's Law of Universal Gravitation as a function of F(r). Where m1 and m2 are the masses in the system and G is the gravitational constant.
Take the integral evaluated from the initial radius to the final radius.
Gravity is a conservative force, so:
To make equations work nicely, we usually state that Ro(initial r) is set at infinity and that the initial potential energy is 0. So it simplifies the above to be:
Which should be the formula you see on your formula chart!
Practice Questions
1. A 5.00 × 10^5-kg subway train is brought to a stop from a speed of 0.500 m/s in 0.400 m by a large spring bumper at the end of its track. What is the force constant k of the spring? (Taken from Lumen Learning)
Answer:
Energy is not conserved because there is acceleration from a force, therefore we can tackle this problem with work!
So we know that W = Fd, and we know our d, so let's try to find the force.
F=ma
We don't know acceleration! But we know our displacement, our initial velocity, and our final velocity...so we can recall an equation from unit 1.
Then we know that W = F*d so:
Another relationship we know about work is:
Spring energy is elastic potential energy so we can plug that formula into the equation.
2. Suppose a 350-g kookaburra (a large kingfisher bird) picks up a 75-g snake and raises it 2.5 m from the ground to a branch. (a) How much work did the bird do on the snake?
(b) How much work did it do to raise its own center of mass to the branch? (Taken from Lumen Learning)
Answer:
(a)
(b)
3.

Taken from CollegeBoard
Answer:
Make sure to use the variables they want you to use and place bounds if they exist in the problem.

4.

Answer:

Browse Study Guides By Unit
🚗Unit 1 – Kinematics
🚀Unit 2 – Newton’s Laws of Motion
🎢Unit 3 – Work, Energy, & Power
🎳Unit 4 – Systems of Particles & Linear Momentum
🚲Unit 5 – Rotation
🌊Unit 6 – Oscillations
🪐Unit 7 – Gravitation
🙏Exam Reviews

Fiveable
Resources
© 2023 Fiveable Inc. All rights reserved.