9.2 Confidence Intervals for the Slope of a Regression Model
6 min read•june 18, 2024
Jed Quiaoit
Josh Argo
AP Statistics 📊
265 resourcesSee Units
Confidence Intervals
As previously stated, there are two kinds of inference: prediction and testing claims. The first type of inference in regards to linear regression we are going to tackle is the prediction model (in other words, confidence intervals). 😎
Confidence intervals are a way to estimate the value of a population parameter based on sample data. They provide a range of values that is likely to contain the true population parameter with a certain level of confidence. For example, if we construct a 95% confidence interval for a population mean, we can be 95% confident that the true population mean lies within the interval. Confidence intervals are useful for making predictions about future samples or for comparing the results of different studies.
The width of the confidence interval depends on the sample size, the level of confidence, and the degree of variation in the sample. A larger sample size, a higher confidence level, and less variation in the sample will result in a narrower confidence interval.
To construct a confidence interval for a population mean, we first need to calculate the standard error of the mean (SEM). The SEM is a measure of the variability of the sample mean. It is calculated as the standard deviation of the sample divided by the square root of the sample size. The SEM gives us an idea of how much the sample mean is likely to vary from the true population mean.
To construct the confidence interval, we then add and subtract a multiple of the SEM from the sample mean. The multiple is chosen based on the desired confidence level. For example, to construct a 95% confidence interval, we would use a multiple of 1.96. So the confidence interval would be the sample mean plus or minus 1.96 times the SEM.
For example, suppose we have a sample of 10 observations with a mean of 10 and a standard deviation of 2. The SEM would be 2/sqrt(10) = 0.6. To construct a 95% confidence interval, we would add and subtract 1.96 times the SEM from the sample mean, resulting in a confidence interval of (8.8, 11.2). This means that we can be 95% confident that the true population mean lies within the interval (8.8, 11.2).
How does this change in the context of this unit (i.e., lines and slopes)? 🤔
In linear regression, our biggest interest is the slope of our regression line. While we can somewhat easily calculate the slope of our sample, we know that this slope is going to change as we add more data points and could change greatly if we were to add several more data points; do instead of just relying on our sample slope, it's a much more robust process to construct a confidence interval to find all possible values of our slope!
Point Estimate
The first part of our confidence interval is our point estimate. This is the exact slope of our sample data that can be calculated using the methods discussed in Unit 2. This is the middle of our confidence interval and our starting point. From there, we are going to add and subtract our margin of error to give us a “buffer zone” around our sample prediction. 📈
Margin of Error
Our margin of error for our confidence interval is calculated by using the appropriate t score and the standard deviation of the residuals and standard deviation of the x values.
Our t score is based on the confidence level and degrees of freedom as mentioned in Unit 7.
Our standard error can be calculated using the formula on the formula sheet (below).
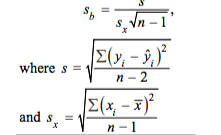
(Note: This formula uses n–2 in the denominator instead of n–1 because two parameters, α and β, must be estimated to obtain the predicted values from the least-squares regression line.)
This formula is very cumbersome and I would always recommend using your graphing calculator to calculate your interval by selecting LinRegTInt and using your L1 and L2 for your sample data. 📱
Side Note: Standard Deviation and Residuals
In linear regression, the sample regression line is an estimate of the population regression line, which represents the underlying relationship between the response variable and the predictor variable in the population. The residuals from the sample regression line are the differences between the observed response values and the predicted response values based on the sample regression line. These residuals can be used to estimate the deviation of the response values from the population regression line. 😃
The standard deviation of the residuals, denoted as s, is a measure of the dispersion of the residuals around the mean. It is calculated as the square root of the sum of the squared residuals divided by n - 2, where n is the sample size. The standard deviation of the residuals can be used to estimate the standard deviation of the deviations of the response values from the population regression line, denoted as σ.
The standard deviation of the residuals is also known as the standard error of the estimate, and it is used to construct confidence intervals and hypothesis tests for the population slope and the population intercept. It can be used to evaluate the fit of the sample regression line and to compare the fits of different regression models.
Conditions
Now, we established that the appropriate confidence interval for the population slope in linear regression is a t-interval, which is based on the t-distribution. Recall from previous units that the t-distribution is a type of probability distribution that is used to estimate population parameters when the sample size is small or when the population standard deviation is unknown.
As with every inference procedure we have covered, there are conditions for inference that must be met if we carry out a test or construct an interval: 📜
(1) Linear
The first and easiest condition to check is that the true relationship between our x and y variable appear to be linear. This can be confirmed by observing the residual plot and seeing that there is no real pattern in the residuals.
(2) Standard Deviation of y
The next condition that must be met is that the standard deviation of y must not change as x changes. In other words, our residual plot does not scatter more or less as we move down the x axis. Again, there is absolutely no pattern on the residual plot
(3) Independence
Independence can be checked two ways:
- Data was taken from a random sample or randomized experiment
- 10% condition (same as other inference procedures): “It is reasonable to believe there is at least 10n… in our population”
(4) Normal
As we have all figured out by now, everything hinges on the normal distribution in statistics. To show normal distribution for quantitative data, we use the Central Limit Theorem, which states that our sample size is at least 30 (or our y values are approximately normal as is).
Once you have checked your conditions, you are good to go in using your sample data to construct and interpret a confidence interval for quantitative means (which I strongly recommend using some form of technology like a graphing calculator to do! Woo-hoo! 🎉
🎥 Watch: AP Stats Unit 9 - Inference for Slopes
Browse Study Guides By Unit
👆Unit 1 – Exploring One-Variable Data
✌️Unit 2 – Exploring Two-Variable Data
🔎Unit 3 – Collecting Data
🎲Unit 4 – Probability, Random Variables, & Probability Distributions
📊Unit 5 – Sampling Distributions
⚖️Unit 6 – Proportions
😼Unit 7 – Means
✳️Unit 8 – Chi-Squares
📈Unit 9 – Slopes
✏️Frequently Asked Questions
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.