📚

All Subjects

📊

AP Stats

📈

Unit 9

9.6 Skills Focus: Selecting an Appropriate Inference Procedure

5 min read•june 18, 2024

Josh Argo

Jed Quiaoit

AP Statistics 📊

265 resources

See Units

One of the most important skills in AP Statistics is being able to identify the best inference procedure to use in order to complete a hypothesis test or confidence interval. We have covered all of the following types of procedures: 📄

One Proportion Z Test
One Proportion Z Interval
One Sample T Test
One Sample T Interval
Matched Pairs T Test
Two Proportion Z Test
Two Proportion Z Interval
Two Sample T Test
Two Sample T Interval
Chi Squared Goodness of Fit Test
Chi Squared Test for Independence
Chi Squared Test for Homogeneity
Linear Regression T Interval
Linear Regression T Test

For example, If given a problem involving one of the linear regression t procedures, it is most common that you will be given a computer output and be asked to make a conclusion or construct an interval.

Here are a couple illustrative flowchart "cheat sheets" on picking the right inferential procedure. Good luck! ⭐

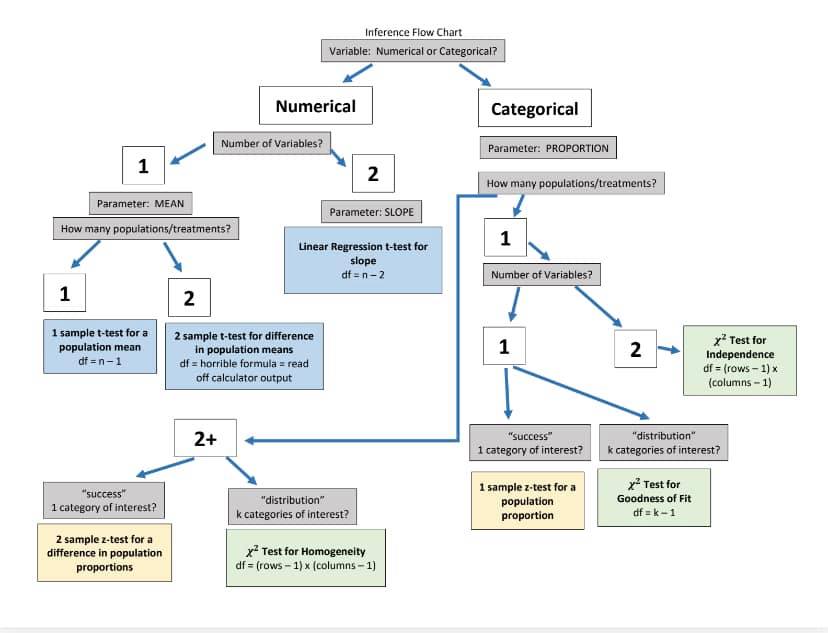
Source: Mr. Sardinha

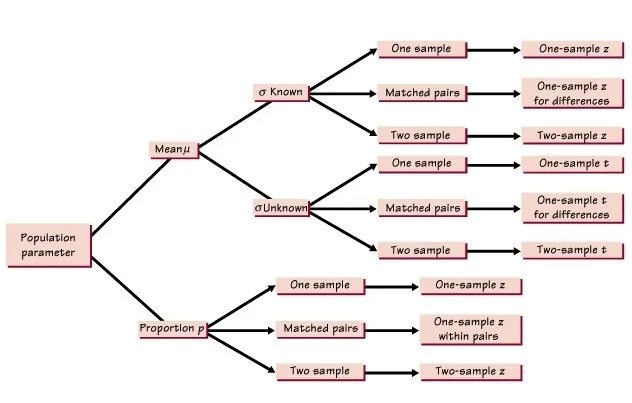
Source: Reddit

Example 1

Here is a computer output similar to what you would see on the AP test. This is based on a study with a sample size of 30.

Remember from Unit 2, that we are only focusing on the inference values associated with the slope, which is the row entitled “Sick Days.”

Confidence Interval

In order to construct a confidence interval like we discussed in Section 9.2, we will need the point estimate (sample slope), t-score and standard error.

Everything except our t-score is given in the computer output, so we have to calculate our t-score based on our confidence level and sample size. We will first calculate our degrees of freedom of 28 and then use that with the invT function to calculate our t-score. We get a t-score of 2.05 for a 95% confidence level.

For the computer output above, our confidence interval would be:

0.962.05(0.12)

Which comes out to be (0.714, 1.206).

In this case, we can be sure that the two variables of interest (sick days and wellness visits) because 0 is not contained in our interval and therefore there is evidence that the two have some correlation. This is also supported by our high r value that could be easily computed by the R2 value.

Hypothesis Test

The other option for inference would be to use the p-value to make a judgment on the hypothesis test. In this example, our p-value for the slope is 0.02, which is usually considered significant enough to reject our null hypothesis.

In this instance, our conclusion would be:

Since our p value 0.02<0.05, we reject the null hypothesis. We have significant evidence that the true slope of the regression model between the number of sick days taken and the number of wellness visits is not 0.

Again, since we have some evidence that the slope is not 0, this shows that these two things are correlated, which is also evidenced by the R2 and resulting correlation coefficient.

Example 2: Pick a Test!

(1) A marketing research firm is interested in determining whether the proportion of adults in the United States who use a certain brand of toothpaste is significantly different from 50%. They survey a random sample of 500 adults and find that 270 of them use the toothpaste. Which of the following tests is/are appropriate to use?

(2) A high school statistics teacher wants to determine whether the mean score on a certain statistics exam is significantly different from 80. They administer the exam to a random sample of 25 students and find that the mean score is 78. Which of the following tests is/are appropriate to use?

(3) A psychology researcher is interested in determining whether there is a significant difference in anxiety levels between a treatment group and a control group. They measure anxiety levels in both groups before and after an intervention and find that the mean difference in anxiety levels between the two groups is -5. Which of the following tests is/are appropriate to use?

(4) A political pollster is interested in determining whether the proportion of registered voters who support a certain candidate is significantly different from 40%. They survey a random sample of 1000 registered voters and find that 400 of them support the candidate. They also survey a random sample of 1000 registered voters from a different region and find that 300 of them support the candidate. Which of the following tests is/are appropriate to use?

(5) A nutritionist is interested in determining whether the mean daily caloric intake of a certain population is significantly different from 2000 calories. They collect data from a random sample of 50 individuals from the population and find that the mean caloric intake is 1950 calories. Which of the following tests is/are appropriate to use?

(6) A historian is interested in determining whether the distribution of birth months among a group of people is significantly different from a uniform distribution. They collect data on the birth months of a random sample of 100 people and find that there are more births in the summer months than in the winter months. Which of the following tests is/are appropriate to use?

(7) A sociologist is interested in determining whether there is a significant association between the type of car a person drives and their political party affiliation. They collect data on the car types and political party affiliations of a random sample of 100 people and find that there are more Democrats who drive sedans than Republicans. Which of the following tests is/are appropriate to use?

(8) A medical researcher is interested in determining whether there is a significant difference in the effectiveness of two different treatments for a certain medical condition. They randomly assign patients to receive either treatment A or treatment B and measure the percentage of patients who show improvement after receiving each treatment. They find that the percentage of patients who show improvement is significantly higher for treatment A than for treatment B. Which of the following tests is/are appropriate to use?

(9) A real estate agent is interested in determining whether there is a significant relationship between the size of a house (in square feet) and its sale price. They collect data on the sizes and sale prices of a random sample of houses and find that there is a positive relationship between the two variables. Which of the following tests is/are appropriate to use?

Answers

(1) One Proportion Z-Test, One Proportion Z-Interval

(2) One Sample T-Test, One Sample T-Interval

(3) Matched Pairs T-Test

(4) Two Proportion Z-Test, Two Proportion Z-Interval

(5) Two Sample T-Test, Two Sample T-Interval

(6) Chi Squared Goodness of Fit Test

(7) Chi-Squared Test for Independence

(8) Chi-Squared Test for Homogeneity

(9) Linear Regression T-Test, Linear Regression T-Interval

🎥 Watch: AP Stats Unit 9 - Inference for Slopes

Browse Study Guides By Unit