1.15 Connecting Limits at Infinity and Horizontal Asymptotes
5 min read•june 18, 2024
AP Calculus AB/BC ♾️
279 resourcesSee Units
Limits at Infinity
In this section, we will focus on understanding the behavior of functions as they approach infinity in the x-direction. We will explore the concept of limits at infinity and how they relate to horizontal asymptotes in a function.
Objectives:
- Interpret the behavior of functions using limits involving infinity in the x-direction.
- Understand the concept of limits at infinity.
- Describe and explain asymptotic and unbounded behavior of functions using limits.
Essential Knowledge:
- The concept of a limit can be extended to include limits at infinity in the x-direction.
- Asymptotic and unbounded behavior of functions in the x-direction can be described and explained using limits at infinity.
When a function approaches a value of positive or negative infinity in the x-direction, the limit is said to be infinite. For example, if a function f(x) approaches positive infinity as x approaches positive infinity, we would write the limit as:
lim x->+infinity f(x) = +infinity
Similarly, if a function approaches negative infinity as x approaches negative infinity, we would write the limit as:
lim x->-infinity f(x) = -infinity
In both cases, the limit does not exist in the traditional sense, as the function does not approach a specific value. Instead, the limit tells us about the behavior of the function as x approaches infinity.
Horizontal asymptotes are another way to describe the behavior of a function as it approaches infinity in the x-direction. A horizontal asymptote occurs when the function approaches a constant value as x approaches positive or negative infinity.
For example, a function with a horizontal asymptote at y = a would be written as:
f(x) = a + 1/x
As x approaches positive or negative infinity, the denominator (1/x) becomes smaller and smaller, causing the value of the function to approach the constant value of a. This results in a horizontal asymptote at y = a.
Looking Further
To further expand on the concept of limits at infinity and horizontal asymptotes, it is important to understand the role of leading terms in a function. The leading term of a function is the term with the highest degree of x. This term determines the behavior of the function as x approaches positive or negative infinity.
For example, in the function f(x) = x^2 + x - 6, the leading term is x^2. As x approaches positive or negative infinity, x^2 becomes much larger than the other terms, causing the function to approach positive infinity. This is why the limit of the function as x approaches positive or negative infinity is +infinity.
In contrast, in the function g(x) = 1/x, the leading term is 1/x. As x approaches positive infinity, 1/x becomes smaller and smaller, causing the function to approach 0. This is why the limit of the function as x approaches positive infinity is 0 and the function has a horizontal asymptote at y = 0.
Finally, it is important to understand that while a function may have a limit at infinity or a horizontal asymptote, this does not guarantee that the function will approach this value. For example, the function h(x) = x^2 + sin(x) approaches positive infinity as x approaches positive infinity, but the function will oscillate between positive and negative values, so it does not have a horizontal asymptote.
Limits at infinity and horizontal asymptotes provide a powerful tool for analyzing the behavior of functions in the x-direction as x approaches positive or negative infinity. By understanding the role of leading terms, we can describe and explain asymptotic and unbounded behavior in a concise and effective way.
Examples
Let's look at some examples to further illustrate the concept of limits at infinity and horizontal asymptotes. Try these six problems and then check your work against the explanations!

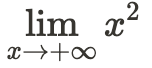
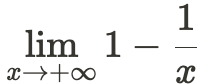



The limit of f(x) = x as x approaches infinity is equal to infinity. This is because as you plug in numbers closer and closer to infinity, the output is closer to infinity.
The limit of f(x) = x^2 as x approaches infinity is equal to infinity. If you take a huge number, like 10,000 and square it, it will only get bigger. Thus, if you "square" infinity, it will equal infinity (just bigger!).
The limit of f(x) = 1 - 1/x as x approaches infinity is equal to 1. Think of just the limit of 1/x under the same conditions. If you continue increasing the size of the denominator, eventually it will equal 0. So, if we go back to our original function with this new knowledge, we can imagine it as 1 - 0 at infinity. Thus, the limit is equal to 1.
The limit of f(x) = (2x^3 - 3x^2 + 4)/(x^3 + 5) as x approaches negative infinity is equal to 2. This means that there is a horizontal asymptote at y = 2. Recall that if the degree of the polynomial is the same in both the numerator and denominator, you should divide the coefficients to find the limit. Even though we're approaching negative infinity, the answer will still be 2 because the negative signs will cancel.
The limit of f(x) = (5x^3)/(x^2 + 3x + 2) as x approaches infinity is infinity. Recall that if the degree of a polynomial is larger in the numerator than the denominator, the limit approaches infinity because the numerator grows faster than the denominator.
The limit of f(x) = (x - 2)/(x - 3) as x approaches 3 from the right is infinity. Imagine evaluating the function at f(4). You would get an answer of 2. Now imagine doing it at f(3.5). That equals 3. Finally, imagine evaluating at f(3.1). That equals 11. See the pattern? Because you are getting closer and closer to x = 3, when you subtract 3 in the denominator, it becomes very, very small. When you divide a number by any number less than 1 (but greater than 0), it's really like multiplying by its inverse. So, the closer the denominator gets to zero, the bigger the result. Therefore, as x approaches 3 from the right, the function will approach positive infinity.
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.