1.6 Determining Limits Using Algebraic Manipulation
3 min read•june 18, 2024
AP Calculus AB/BC ♾️
279 resourcesSee Units
🎥Watch: AP Calculus AB/BC - Algebraic Limits
This topic focuses on the ability to manipulate a limit in order to solve it. Usually, this involves factoring and dividing common factors of rational functions or using alternate forms of trigonometric functions. You can find example problems for all algebraic manipulations below.
Example Problem: Determining a Limit Using Factoring
.png?alt=media&token=73f202ce-ffb6-44b9-a521-63ae0b58ffc9)
At first, you might want to plug in infinity because that is what we learned earlier in the unit. However, because you have variables on both the top and bottom, you’ll get infinity over infinity. 🧐
To determine the limit, we can factor out an x^2. In other words, we divide each term by x^2. Now, all of the terms except the first terms have an x or x^2 in the denominator. Because of this, we can now plug in infinity. The limit of the terms with a variable in the denominator will be zero. We can assume this because as the number in a denominator approaches infinity, the entire fraction approaches zero. Now, we are left with 5 in the numerator and 7 in the denominator. Thus, the limit is 5 / 7.
As you can see from the example problem, the other powers don't matter because they’re all going to disappear. The “other powers” in the example above would be (-3x + 1) in the numerator and (x - 12) in the denominator. Because they aren’t the highest power in the limit, they won’t affect the eventual limit as much as the highest-powered term. As a rule of thumb use the following rules when evaluating limits the limit of a rational expression as x approaches infinity.
- If the highest power of x in a rational expression is in the numerator, then the limit as x approaches infinity is infinity. ♾️
- If the highest power of x in a rational expression is in the denominator, then the limit as x approaches infinity is zero. ⭕
- If the highest power of x in a rational expression is the same in both the numerator and denominator, then the limit as x approaches infinity is the coefficient of the highest term in the numerator divided by the coefficient of the highest term in the denominator. This is the rule we could use in the example above. Because the highest power was x^2 in both the numerator and denominator, the limit as x approaches infinity is 5 / 7. ➗
Example Problem: Determining a Limit Using Alternate Forms of Trigonometric Functions
On the AP Exam, you’ll be expected to recall the limits of common trigonometric functions. Below are the most common formulas you’ll be expected to remember. 📏
.png?alt=media&token=f60e7f75-0b51-48fe-9b25-8ab7b5e4a9ac)
To better understand these formulas, let’s discuss them individually.
Rules #1 and #2:
These two rules are pretty much the same as what we would do for any limit. The first way to solve a limit is to plug in the x value into the function. In the formulas above, the value “c” is being plugged in to try and determine the limit. If you are asked to find the limit of sin(x) as x approaches 1, then you simply plug in 1 and get your answer.
Rule #3:
This rule is VERY common in AP Calculus. Moving forward, you should be on the lookout for this rule.
.png?alt=media&token=6f433e1b-30d9-4b81-8568-10322e48d4f5)
If you’re asked to find the limit of the function above, you can use the third rule to help you. Because you know that the limit as x approaches 0 of (sin(x)/x) = 1, you can assume that the limit as x approaches 0 of (sin(4x)/x) is 4 times that. Thus, your answer would be 4.
Rule #4:
This last rule is not as common as rule #3 but it's still just as important. To understand this rule, look at the example below.
If you’re asked to evaluate the following limit, you can use this rule.
.png?alt=media&token=7454c08c-b334-4fcb-9d46-f2b1be62c28b)
Because sec x = 1/(cos(x)), you can use the following steps to solve the limit.
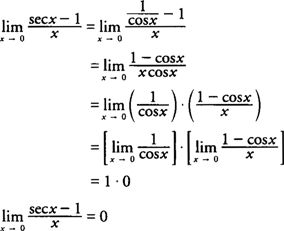
CliffsNotes
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.