1.10 Exploring Types of Discontinuities
5 min read•june 18, 2024
AP Calculus AB/BC ♾️
279 resourcesSee Units
Discontinuities
🎥Watch: AP Calculus AB/BC - Continuity, Part II
This is the first topic dealing with continuity in unit 1. Until this point, our main focus was limits and how to determine them. However, a large part in finding and determining limits is knowing whether or not the function is continuous at a certain point. In topics 1.9 - 1.13, we will discuss continuity and different types of discontinuities you will see on the AP Exam.
There are four types of discontinuities you have to know: jump, point, essential, and removable.
Jump Discontinuity ↔
If the left and right-handed limits aren’t equal, then the double-handed limit does not exist (DNE). In this scenario, we would have a jump discontinuity. The graph of that would look something like this:

Math Warehouse
As you can see, there is a break in the physical continuity of the graph at x. If the limit from both sides is different, how can we find a specific value that the function approaches? We cannot. Thus, the limit DNE.
Point Discontinuity 🕳
A point discontinuity occurs when the function has a “hole” in it from a mission point because the function has a value at that point that is “off the curve.”

Wikipedia
Essential Discontinuity ♾️
An essential discontinuity occurs when the curve has a vertical asymptote. This is also called an infinite discontinuity.
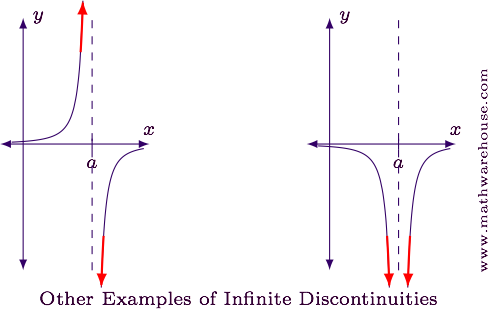
Math Warehouse
Removable Discontinuity 🚫
This last discontinuity is fairly common. A removable discontinuity occurs when you have a rational expression with a common factors in the numerator and denominator. Because these factors can be cancelled, the discontinuity is “removable.”

Now for a closer look at discontinuities.
Jump discontinuities occur when the left and right-handed limits of a function are not equal, resulting in the double-handed limit not existing (DNE). This can be visualized as a break in the physical continuity of the graph at a certain point. The graph of a function with a jump discontinuity would look like a step function, with the function abruptly jumping from one value to another at the discontinuity point.
Point discontinuities occur when the function has a "hole" in it at a certain point, meaning that the function has a value that is "off the curve". This can be visualized as a small gap in the graph of the function at the discontinuity point.
Essential discontinuities occur when the curve of a function has a vertical asymptote, also known as an infinite discontinuity. This can be visualized as the function approaching closer and closer to a certain value, but never reaching it. The graph of a function with an essential discontinuity would have a vertical line at the discontinuity point.
Removable discontinuities occur when a function is a rational expression with common factors in the numerator and denominator. These common factors can be canceled, making the discontinuity "removable". This can be visualized as a hole in the graph of the function at the discontinuity point that can be filled in.
It's important to note that these types of discontinuities are not mutually exclusive and some functions may have more than one type of discontinuity. Also, it's worth noting that, in real life, a discontinuity may have a physical meaning; for instance, a jump discontinuity in a temperature curve may indicate a change of phase.
To practice identifying these types of discontinuities, you can try working through examples from your textbook, online resources such as Khan Academy, or by using interactive tools such as graphing calculators or computer programs. You can also try creating your own examples and working through them to get a better understanding of the process. Continuity is a fundamental concept in Calculus, and by understanding how to identify and analyze different types of discontinuities, you will be well-prepared to succeed in your studies of Calculus.
Here are some examples to help you practice:
Example 1: Determine the type of discontinuity of the function f(x) = 1/x at x = 0.
Solution: The function f(x) = 1/x has a vertical asymptote at x = 0. This is an essential discontinuity, as the function approaches closer and closer to a certain value but never reaches it.
Example 2: Determine the type of discontinuity of the function f(x) = x^2 sin(1/x) at x = 0
Solution: The function f(x) = x^2 sin(1/x) is not defined for x=0. As x approaches 0, the function oscillates between positive and negative values, so the left and right limits do not exist. At this point, the function has a hole in it and the limit does not exist. This is an essential discontinuity.
Example 3: Determine the type of discontinuity of the function f(x) = sqrt(x^2 - 4) at x = 2.
Solution: The function f(x) = sqrt(x^2 - 4) is not defined for x = 2. At this point, the function has a hole in it. This is a point discontinuity.
Example 4: Determine the type of discontinuity of the function f(x) = (x^2 - 4) / (x - 2) at x = 2.
Solution: The function f(x) = (x^2 - 4) / (x - 2) is not defined for x = 2. However, if we factor the numerator and denominator, we can cancel the factors (x-2) from both numerator and denominator. This makes the discontinuity "removable" and this is a removable discontinuity.
Example 5: Determine the type of discontinuity of the function f(x) = sin(1/x) at x = 0.
Solution: The function f(x) = sin(1/x) approaches different values as x approaches 0 from different sides. The limit from the left is 1 and from the right is -1. This is a jump discontinuity.
In conclusion, understanding the different types of discontinuities and how to identify them is an important skill in Calculus. Jump, point, essential, and removable discontinuities are the four types of discontinuities that you need to know for the AP Calculus Exam. Jump discontinuities occur when the left and right-handed limits of a function are not equal, resulting in the double-handed limit not existing (DNE). Point discontinuities occur when the function has a "hole" in it at a certain point, meaning that the function has a value that is "off the curve". Essential discontinuities occur when the curve of a function has a vertical asymptote, also known as an infinite discontinuity. Removable discontinuities occur when a function is a rational expression with common factors in the numerator and denominator. These common factors can be canceled, making the discontinuity "removable".
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.