1.5 Determining Limits Using Algebraic Properties of Limits
3 min read•june 18, 2024
Anusha Tekumulla
AP Calculus AB/BC ♾️
279 resourcesSee Units
🎥Watch: AP Calculus AB/BC - Algebraic Limits
This topic focuses on using the properties of limits to determine a limit value. We refer to these properties as algebraic because they are essentially the same properties you learn in algebra. Below, you’ll find a list of properties of limits:
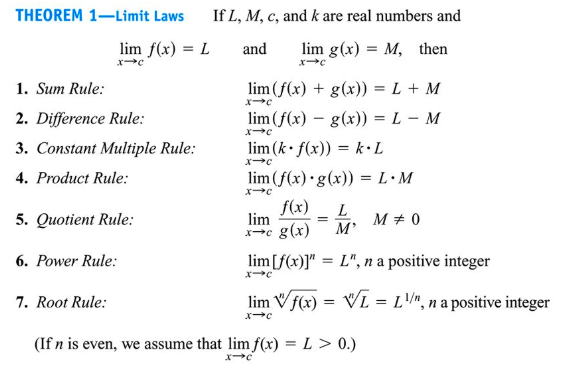
Medium.com
Here are some example problems to better understand the limit properties:
Example Problem: Using the Sum Rule to Determine a Limit ➕
.png?alt=media&token=ed58f5d3-6506-4326-96c7-97d2e9da382c)
Answer: 36
Explanation: In this example, we need to use the sum rule. Our first function is x^2 and our second function is x^3. Because the functions are being added together, we can evaluate their limits separately. The limit of x^2 as x approaches 3 is 9. The limit of x^3 as x approaches 3 is 27. Thus, the limit of (x^2 + x^3) as x approaches 3 is 9 + 27 = 36. The sum rule is very similar to the difference rule. If the function was x^2 - x^3, we would use the difference rule and the answer would be 9 - 27 = -18.
Example Problem: Using the Constant Multiple Rule to Determine a Limit ➡
.png?alt=media&token=b87e5e5b-b1aa-4f38-9da3-8faec1faad72)
Answer: 1500
Explanation: In this example, we need to use the constant multiple rule. We can separate the constant (12) from the function (x^3). With the constant out of the way, we can solve the limit. The limit of x^3 as x approaches 5 is 125. Thus, the limit of (12x^3) as x approaches 5 is 125 * 12 = 1500.
Example Problem: Using the Product Rule to Determine a Limit ✖️
.png?alt=media&token=860add48-f710-4170-9077-992d8a1304c1)
Answer: 1620
Explanation: In this example, we need to use the product rule. We can separate the first function (12x^3) from the second function (27x^-2). The limit of the first function as x approaches 5 is 1500 (from the previous example). The limit of the second function as x approaches 5 is 27 ⁄ 25 = 1.08. Thus the limit of (12x^3 * 27x^-2) as x approaches 5 is 1500 * 1.08 = 1620.
The difference rule is essentially the same as the product rule. If the function in this example were 12x^3 / 27x^-2, we would use the difference rule and the answer would be 1500 / 1.08 = 1388.889.
Example Problem: Using the Exponent/Power Rule to Determine a Limit 💥
.png?alt=media&token=134a240c-70c0-4477-8a2d-d59a23293cda)
Answer: 729
Explanation: In this example, we need to use the power rule. We can separate the function (12x3) from the exponent. The limit of the function as x approaches 5 is 9. Now, we just have to apply the exponent to the answer. Thus the limit of (x + 4)^3 as x approaches 5 is 9^3 = 729.
The root rule is essentially the same as the power rule. If the function in this example were ∛(x + 4), we would use the root rule and the answer would be ∛9 = 2.08
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.