Dalia Savy
Jacob Jeffries
AP Chemistry 🧪
269 resourcesSee Units
Some of this section gets a little advanced. If you don't know calculus or get confused with some of the more complex math used in this study guide, don't worry! Outside of the stuff you learned in the last section about rate laws, you don't need to know how to derive anything, just know how to apply the formulas for rate laws and integrated rate laws and understand in a basic sense how they work! We've bolded the important stuff to know for the AP Exam.
The Math Behind the Rate Law
As mentioned before, the reaction order is described by the variable n. This notation is used because n typically describes an integer value in science and mathematics, and the order of a reaction is typically an integer, however, it does not have to be an integer.
One such example is Michaelis–Menten kinetics, which is one of the most commonly known kinetic models in biochemistry. The specific details are not important, however, for biology aficionados, the general reaction that these kinetics describe is:

In this case, E is an enzyme (a specific category of a catalyst, which will be studied further in this unit), S is a substrate, and P is a general product. These reactions typically have a fractional reaction order in certain cases. Notice that the enzyme is regenerated by the reaction as if it were never consumed by the reaction in the first place.
Though, typical chemical reactions retain integer values for their reaction order. For the purposes of the AP exam, we will only discuss the n = 0, n = 1, and n = 2 cases in-depth. However, for those proficient in calculus, we will solve the problem for the general case (such that n ≠ 1).
As mentioned before, the order describes how the amount of molecules present, aka concentration, affects the reaction rate. In order to investigate this further, we must motivate the idea of a concept called a rate law. To make the mathematics intuitive, let’s imagine the idea of population dynamics. For a population in a crisis, the population as a function of time is modeled as decaying exponentially:
In this case, P0 is the initial population, t is time, and t1/2 is the half-life of the population, which is how long it takes for a population to reach half its initial population.
For reasons motivated by calculus, we express the base of the exponential as the number e:

This equation should be somewhat intuitive. In the case of the crisis being a disease, as more people die, the number of disease carriers decreases, which means fewer and fewer people can be affected as time goes on, leading to both a decrease in population along with a decrease in how fast the population is decaying (Fig. 1).
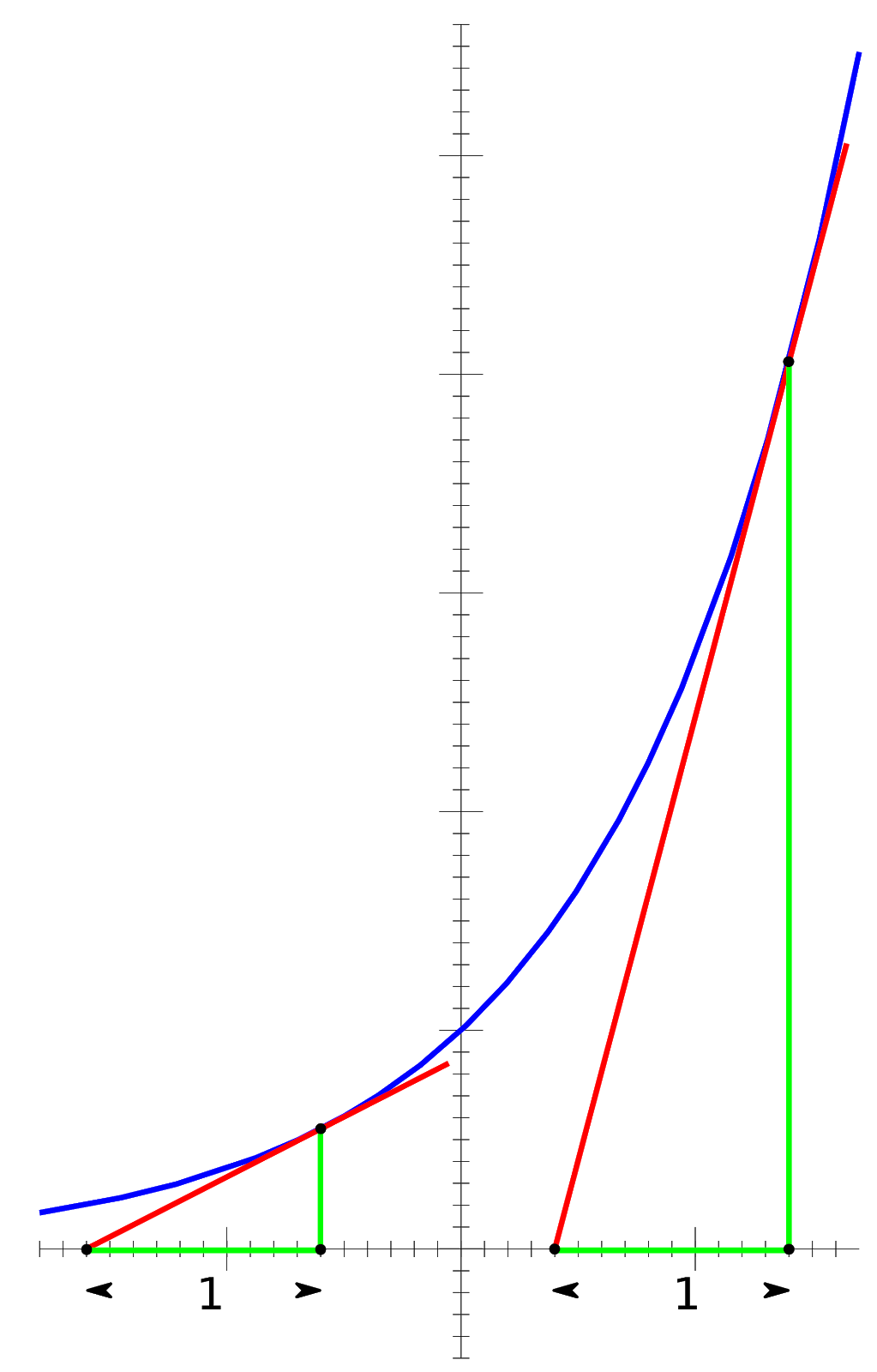
Fig 1: Exponential Growth and Instantaneous Rates. Note that this figure does not model the above situation, but rather the opposite, the case of Pe^kt, where k is positive, leading to exponential growth
In the above figure, the slopes of the red tangent lines represent the instantaneous rates of change. One can see that, as the graph itself increases in value, so does the rate of change of the graph. This concept is easily reversed to represent population decay, as population decay is exponential decay instead of exponential growth.
A very important property of exponential functions is that the rate of change of an exponential function is proportional to itself:
.png?alt=media&token=9a2b7b26-2c70-4c11-bed2-e4ce85de6205)
While slightly morbid and dark, this same concept can be applied to chemical reactions. As the reaction progresses, fewer and fewer atoms are able to react with one another, so there are analogously fewer disease carriers to spread the aforementioned fatal disease.
Connecting to Chemistry
Connecting this concept to chemistry, let's consider the simple reaction A → B. We model the rate of the reaction as the rate of the formation of B, which is also the same as the rate of the depletion of A. As previously established, this relationship is shaped like an exponential decay curve, thus we can logically arrive at the following equation: Rate = k[A]. However, this is only true for the n = 1 case. For any n: Rate = k[A]^n. This is simply called a rate law of order n with rate constant k.
If we invoke calculus notation for rates of change, those proficient in calculus will recognize the equation as a separable differential equation:
If you, the reader, do not know calculus and/or are not comfortable with the technique of separation of variables, don't worry, as it is not necessary for the AP exam. Feel free to skip to the end of this section to the next bold text if you don't want to see the derivation of the integrated rate laws. However, for those that are comfortable with the technique, we can solve for the concentration of A as a function of time:
.png?alt=media&token=c9820e01-4a3d-49b3-9bd9-b11e8f8241ec)
.png?alt=media&token=865805f3-3d05-4837-81a9-c00f28363599)
To solve for the constant of integration C, we will use the notational condition that [A](0) = [A]o, which is simply the concentration before the reaction proceeds.
.png?alt=media&token=9be5c4c3-645e-4f14-a50f-60edb17263b7)
Because of the condition set by Eq. 25 (n ≠ 1), we will analyze the above equation for the n = 2 case:
.png?alt=media&token=f12c21af-8a1d-4df5-9c42-9cb21f4ab0c1)
We can divide both equations by a factor of -1 and use properties of powers to come up with the following equation:
.png?alt=media&token=a6ae3329-8e95-492a-9dd8-6e7321a6a552)
Eq. 29 is the same equation as the one on the official AP formula sheet and is known as the second-order integrated rate law, where [A] is the final concentration, [A]₀ is the initial concentration, k is the rate constant, and t is the elapsed time. The first-order integrated rate law is ln([A]) - ln([A]₀) = -kt. These equations can be used to calculate the rate law, based on reaction order and the rate constant (which is temperature dependent).
Integrated Rate Laws
An important concept is that these equations can be put onto a graph to produce a linear relationship. From an established linear relationship, we can solve for the rate constant k.
A linear relationship between two variables y and x is defined by a familiar equation from algebra:
.png?alt=media&token=72a699cc-a902-4e08-9d99-e04be32a00db)
Analyzing the integrated rate law for n = 0,:
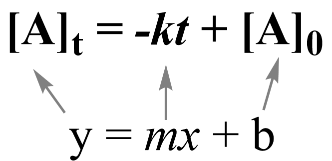
Image Courtesy of Chemistry Steps
for n =1,:
.png?alt=media&token=f9697394-dd7a-428a-aff5-fdc888ad7c24)
and for n = 2:
.png?alt=media&token=645ddd9a-5069-4360-8ed1-88c3e072010a)
We can logically derive a set of qualitative information:
- For a zeroth-order reaction, the graph of [A] vs. time is linear with a slope -k. In a zeroth order reaction, rate is constant, so R = k implies that concentration will change at a constant rate, which implies a linear relationship.
- For a first-order reaction, the graph of ln[A] vs. time is linear with a slope of -k.
- For a second-order reaction, the graph of 1/[A] vs. time is linear with a slope of k.
This will likely be information that is necessary to determine the order of a reaction, which has come up on free-response questions several times!
Example Question
For the reaction A → B, the following graphs are shown:

a) What is the rate law for the reaction? Represent the rate constant as k, not a numerical value. Explain how you arrived at your answer
b) Estimate the value of k for this reaction. Show all work.
c) If the initial concentration of A is 0.200 M, what is the concentration remaining after 30 seconds?
Answers
a) We see that the reaction is linear on the rightmost graph, which is 1/[A] vs time, meaning that the reaction is second order in A, making the rate law R = k[A]² (+1 for the answer, +1 for explanation with linear relationship).
b) The points (0, 5) and (200, 25) can be seen on the graph, meaning k = 25 - 5/200-0 = 20/200 = 0.1 Lm⁻¹s⁻¹ (+1 for setting up a slope equation, +1 for correct answer with correct units)
c) We can use the second-order integrated rate law:
1/[A] - 1/[A]0 = kt
1/[A] - 1/0.200 = 0.1(30)
1/[A] = 0.1(30) + 1/0.200 = 8
[A] = 0.125M (+1 for setup, +1 for answer with units)
Half-Life in First-Order Reactions
Half-life is defined as the time it takes for the concentration of a substance to decrease by half. This concept goes into nuclear chemistry, which is not included in the AP Chemistry curriculum but is important in first-order reactions.
Half-life is related to the rate constant (k) of a first-order reaction by the equation: t1/2 = 0.693/k. This equation can be used to determine the half-life of a substance if the rate constant for the reaction is known, or to determine the rate constant if the half-life is known. The most important thing to note is that for a first-order reaction, the half-life is constant.
The equation for the half-life of a first-order reaction (t1/2 = 0.693/k) is on the reference table given to you on the AP Chemistry exam!
Browse Study Guides By Unit
⚛️Unit 1 – Atomic Structure & Properties
🤓Unit 2 – Molecular & Ionic Bonding
🌀Unit 3 – Intermolecular Forces & Properties
🧪Unit 4 – Chemical Reactions
👟Unit 5 – Kinetics
🔥Unit 6 – Thermodynamics
⚖️Unit 7 – Equilibrium
🍊Unit 8 – Acids & Bases
🔋Unit 9 – Applications of Thermodynamics
🧐Exam Skills
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.