D
Dalia Savy
D
Dylan Black
AP Chemistry 🧪
269 resourcesSee Units
To learn how to write out rate laws, let's refresh ourselves on what exactly a rate law is. Given a reaction A → B, the rate law for this reaction is R = k[A]ⁿ, where R is the reaction rate, k is the rate constant, and n is the order of the reaction in A. The rate law shows us that rate is directly proportional to the concentration of the reactants, or in this case just the single reactant.
Rate laws are simply what they look like: mathematical expressions to find the rate of a reaction. However, given any reaction, is there a way to find exactly what the rate law is? Let's find out!
Rate Laws Found Experimentally
Unfortunately, the only true way that rate laws can be found is through an experiment. It's a common mistake of chemistry students to look at the stoichiometric coefficients of the reactants and use those as reaction orders, but you cannot do that!
The reaction 2A → B is not necessarily second order, it could be, but we won't know until we run an experiment. The experiment run to find a rate law is quite simple. All it involves is running multiple trials of a reaction with different concentrations of each reactant, typically doubling one, and then seeing how the rate reacts to this change in concentration.
One important stipulation is that these reactions must and I mean must be run at the same temperature. If the temperature fluctuates, the rate can change dramatically, giving incorrect results. This is because k, the rate constant, is temperature dependent. Once you find the orders of a reaction, you can plug in values from an experiment to find k.

GIf Courtesy of GIPHY
How Does Concentration Affect Rate?
You might be wondering, how does doubling the concentration change the rate? Well, let's take a look at a general example. Let's say that when the concentration of the reactant is 1 M, the rate of the reaction is 1 mol/Ls, but when the concentration of the reactant is 2 M, the rate of reaction, at the same temperature, is 4 mol/Ls. This means that by doubling the concentration, the rate quadrupled. This is a quadratic effect. Essentially, if R = k[A]ⁿ and doubling [A] leads to a quadrupling in rate, n must be two. We can see this through some simple algebra:
1 = k[A]ⁿ and 4 = k(2[A])ⁿ ==> 4 = k(4[A]²) ==> 1 = k[A]²
As a general rule of thumb: if doubling [] leads to rate doubling, it's first order, quadrupling rate means second order, octupling rate means 3rd order, etc., though it's rare to see more than 2nd order reactions.
Example Problem
Find the rate law for the reaction 2NO + 2H₂ → N₂ + 2H₂O given the reaction data below at 1280 °C.
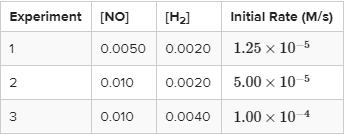
Finding Order of NO
Between experiments 1 and 2, [NO] doubles and [H₂] remains constant, so we can use these to find the order of the reaction with respect to NO. When [NO] is doubled, the rate increases by a factor of 5.0/1.25, which is 4 (we can cancel out the 10⁻⁵ here). Therefore, the reaction is second order with respect to NO.
Finding Order of H₂
Similarly, between experiments 2 and 3, [NO] remains constant and [H₂] doubles. Therefore, we can do the same as before: [H₂] doubles, and the rate increases by a factor of 1 * 10⁻⁴/5 * 10⁻⁵ = 2. Thus, the reaction is first order with respect to H₂.
Finding k and putting it all together
We now know the rate law is in the form R = k[NO]²[H₂]. Now, by plugging in values you can find k and write out the full rate law. Give it a try! The first two steps really are the hard parts.
Elementary Reactions
Okay, but wait...this key topic is titled "Elementary Reactions," but I don't even know what those are yet. An elementary reaction is a chemical reaction that occurs in a single step and involves only a single molecule or a group of atoms. It is the most basic type of chemical reaction and is the starting point for understanding more complex reactions. Everything in this study guide applies to an elementary reaction, and we will discuss more complex reactions throughout the rest of this unit.
As we've seen, elementary reactions can be either first-order or second-order, depending on whether the rate of the reaction is dependent on the concentration of one species or two. Some specific examples of elementary reactions include the reaction of hydrogen and oxygen to form water, the decomposition of ozone, and the ionization of a gas.
AP Practice Question - 2017 #2
The following question was posted by College Board and is part of question two on the free-response section of the 2017 AP Chemistry exam.
The ammonium salt of isocyanic acid is a product of the decomposition of urea, CO(NH₂)₂, represented by the following chemical equation: CO(NH₂)₂ (aq) ⇌ NH₄⁺ (aq) + OCH⁻ (aq)
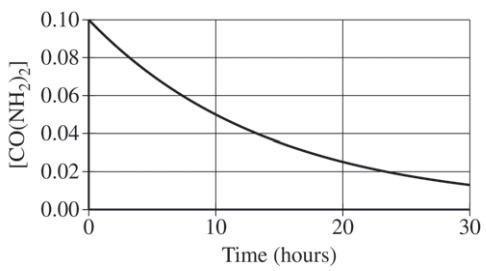
A student studying the decomposition reaction runs the reaction at 90°C. The student collects data on the concentration of urea as a function of time, as shown by the data table and the graph below.
| Time (hours) | [CO(NH₂)2] |
| 0 | 0.1000 |
| 5 | 0.0707 |
| 10 | 0.0500 |
| 15 | 0.0354 |
| 20 | 0.0250 |
| 25 | 0.0177 |
| 30 | 0.0125 |
(e) The student proposes that the rate law is rate = k[CO(NH₂)₂]. (i) Explain how the data supports the student's proposed rate law. (ii) Using the proposed rate law and the student's results, determine the value of the rate constant, k. Include units in your answer.
(f) The student learns that the decomposition reaction was run in a solution with a pH of 13. Briefly describe an experiment, including the initial conditions that you would change and the data you would gather, to determine whether the rate of the reaction depends on the concentration of OH⁻(aq).
Answer to FRQ 2017 #2e-f
Part e, i
For the first part of part e, we are trying to find evidence of this reaction being a first-order reaction. There are two ways we can do that:
- Look for a graph of ln[CO(NH₂)₂] vs. time and identify it as linear, with a slope of -k.
- Identify the half-life of the reaction as constant.
Here, we are given a graph, but it is not linear. Therefore, we have to take a look at the half-life. To recall, the half-life is defined as the time it takes for the concentration of a substance to decrease by half. The easiest way to do this is to think:
- Okay so before the experiment started, the concentration of CO(NH₂)₂ was 0.1000 M. After one half-life, there would be 0.0500 M of CO(NH₂)₂ remaining.
- How long did it take for there to be 0.0500 M of CO(NH₂)₂? According to the provided graph, it took 10 hours.
- To check if something is constant, we have to see if the next half-life is 10 hours as well. Half of 0.0500 M is 0.0250 M, which is the concentration of CO(NH₂)₂ left after 20 hours. It took 10 hours to half its concentration again, meaning the half-life of the reaction is constant! This confirms the student's rate law.
The scoring guidelines posted by College Board gave one point for a correct explanation. Below is a sample response:
"From inspecting the data table or the graph, it is evident that the decomposition reaction has a constant half-life, which indicates that the reaction is a first-order reaction.
Part e, ii
Now that we've got our confirmed rate law, we have to solve for k. In order to do this, you can use the information you've gathered from the last part: this reaction is first-order and its half-life is 10.
Remember, t1/2 = 0.693/k, so all we have to do is plug 10 in for t1/2 and solve for k. There is another way to do this problem just in case you forget about this method. You can rather solve for k by using the integrated rate law for a first-order reaction. Both of these equations are on the given reference sheet, but they are not labeled for you.
Once you get your answer, be sure to add a unit! Since this is a first-order reaction, you know that the units should be s⁻¹. But this is where they trick many students. The time, in this question, was in the units of hours, so your units must be hours⁻¹, or h⁻¹. Below is a sample response provided by College Board.

Part f
This part may seem intimidating since it is asking you to describe an experiment, but you only have to do so briefly. As long as you give them what they ask for, you can gain full credit. The following is a sample response that would earn a full point of credit:
"Perform the experiment at a different concentration of OH⁻ (aq) and measure how the concentration of CO(NH₂)₂ changes over time. Other variables, such as temperature, should be held constant."
Browse Study Guides By Unit
⚛️Unit 1 – Atomic Structure & Properties
🤓Unit 2 – Molecular & Ionic Bonding
🌀Unit 3 – Intermolecular Forces & Properties
🧪Unit 4 – Chemical Reactions
👟Unit 5 – Kinetics
🔥Unit 6 – Thermodynamics
⚖️Unit 7 – Equilibrium
🍊Unit 8 – Acids & Bases
🔋Unit 9 – Applications of Thermodynamics
🧐Exam Skills
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.