📚

All Subjects

🧪

AP Chem

👟

Unit 5

5.8 Reaction Mechanism and Rate Law

7 min read•june 18, 2024

Dylan Black

Dalia Savy

AP Chemistry 🧪

269 resources

See Units

Before we start learning about how to use mechanisms to find something out about the rate of a reaction, let's do a quick refresher on what exactly a mechanism is. A mechanism describes the steps of a reaction as it takes place from reactants to products. It's important to note that mechanisms tell us exactly what happens in a reaction, as the vast majority of reactions happen in many steps.

Review of Mechanisms

When you see a reaction A → B, there are typically multiple steps that lead to A yielding B. This could mean A reacting with an intermediate, or the reaction being catalyzed. Either way, each step is known as an elementary steps, and when you add all of the elementary steps of a mechanism together, you will get the overall balanced chemical equation.

Elementary Steps

Let's take a look at an example mechanism and break it down:

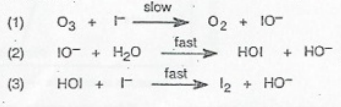
This is the mechanism for the reaction: O₃ + 2I⁻ + H₂O → O₂ + I₂ + 2OH⁻. How did we find that out? Well, if you add up all of the steps of a mechanism, it must and always will add up to the overall reaction.

In this mechanism, there are three elementary steps:

In the first step, ozone and iodide slowly react to form molecular oxygen and iodite ions.
In the second step, the formed iodite ions react with water molecules to form hypoiodous acid and hydroxide ions.
In the last step, the formed hypoiodous acid from the previous elementary step reacts with iodide to form molecular iodine and more hydroxide ions.

Catalysts and Intermediates

Breaking this down helps us identify any possible intermediates or catalysts. Since there are no chemical substances that go into the mechanism and come out without being affected, there are no catalysts.

However, there are two intermediates in this mechanism. Can you identify them? Intermediates are species that are formed during a reaction and then go on to participate in further reactions. When comparing the first step to the second step, we can find that iodite is one of the intermediates. When comparing the second to the third, we can also see that hypoiodous acid is the second intermediate!

👉 If you'd like a review on any of this material, check out the previous guide that explained how to identify the components of a reaction mechanism.

Rate-Determining Steps

Now that we've been refreshed on what mechanisms are, let's start discussing rate laws and how to write the rate law using a mechanism. When writing the rate law of a mechanism, we need to identify the rate-determining step. The rate-determining step is the slowest step of a mechanism. This step essentially constrains how fast the reaction can go!

From here, we can use the stoichiometric coefficients of the slowest step in the mechanism to find the rate law. It is important to note that besides mechanisms, rate laws must be determined experimentally. In fact, problems often are formatted along the lines of, "The mechanism for a reaction is {mechanism}. If {rate law} is the experimentally determined rate law, is this mechanism valid?" Since the overall rate law of a reaction must be found experimentally, it can be used to verify mechanisms.

Example Free-Response Question

Let's break down this idea and put it into practice with an AP Chemistry free-response question (FRQ). The following question is #6 from the 2019 AP Chemistry exam posted online by College Board.

Understanding Basic Rate Laws

Nitrogen dioxide, NO₂ (g), is produced as a by-product of the combustion of fossil fuels in internal combustion engines. At elevated temperatures NO₂ (g) decomposes according to the equation below.

2 NO₂ (g) → 2 NO (g) + O₂ (g)

The concentration of a sample of NO₂ (g) is monitored as it decomposes and is recorded on the graph directly below. The two graphs that follow it are derived from the original data.

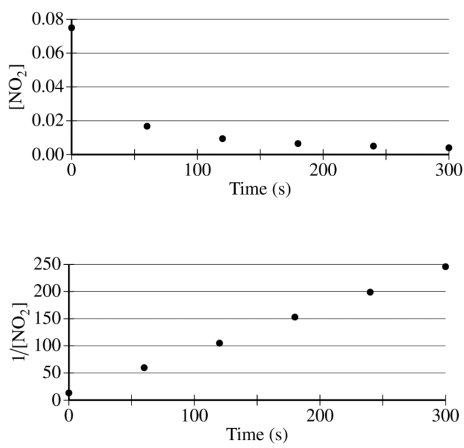
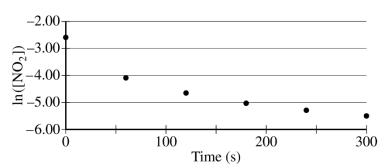
(a) Explain how the graphs indicate that the reaction is second order.

(b) Write the rate law for the decomposition of NO₂ (g).

These two parts were reviewed in earlier study guides within this unit, but let's break them down. For part a, all you have to do is identify that the graph plotting 1/[NO₂] versus time is linear. To review this concept, be sure to check out our study guide about concentration changes over time.

Part a Sample Response: The linear graph of 1/[NO₂] vs. time indicates a second-order reaction."

For part b, take a look at the chemical equation, and write the rate law for the decomposition of NO₂. To review this process, check out our study guide introducing the concept of the rate law.

Part b Sample Response: Rate = k[NO₂]²

Understanding Rate-Determining Steps

The second half of this 2019 FRQ tests your knowledge regarding how to verify a mechanism. Part (c) asks you to consider two possible mechanisms for the decomposition reaction:

(c.i) Is the rate law described by mechanism I shown below consistent with the rate law you wrote in part (b)? Justify your answer.

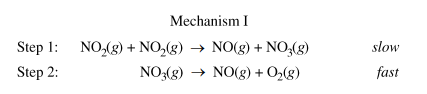
Part b gave us an experimentally determined rate law, so now we have to figure out what the rate law is of the mechanism above and explain if they are the same. Remember that when looking at a mechanism, we have to use the stoichiometric coefficients of the reactants in the slow step, or the rate-determining step. In this mechanism, the RDS is step 1.

Then, we find the rate law to be R = k[NO₂][NO₂], or Rate = k[NO₂]², which matches the experimentally determined rate law.

Part c.i Sample Response: Yes. Step 1 is slow, therefore it is the rate-determing step of this mechanism. The rate law of this elementary reaction is rate = k[NO₂][NO₂] = k[NO₂]², which is consistent with the second-order rate law in part (b).

Experimental Rate Laws vs. Mechanisms

The reason we look at verifying rate laws rather than finding rate laws directly from mechanisms is that the rate law for a reaction can only be determined experimentally as we saw in previous study guides. Rather, an experimentally determined rate law can help chemists verify a mechanism. If the proposed mechanism does not match the experimental rate law, we know that the mechanism cannot be true!

Using Keq to Find the Rate Law

The second half of part c has to do with intermediates. Let's break it down and take a look.

(c.ii) Is the rate law described by mechanism II shown below consistent with the rate law you wrote in part (b)? Justify your answer.

Using our rules from before, we find the slow step and write out our rate law as R = k[N₂O₄]. Boom, done. Wait... let's take a second look there. If we look at the overall reaction (this was given originally in the FRQ), it is 2NO₂ → 2NO + O₂. Therefore, R = k[N₂O₄] is not the rate law! We can rely on the experimentally derived rate law to be the correct one, especially since this question is asking if the mechanism is correctly representing that rate law.

This can be explained by seeing that N₂O₄ is an intermediate for this mechanism. Since intermediates are not reactants, you cannot have an intermediate in your rate law.

So then, how do we go about finding the rate law? This math involves a topic in chemistry that you most likely learned called equilibrium. The first step is a "fast equilibrium," meaning that the reactants constantly react to form the products, and the products constantly react to form the reactants.

We can use this concept to solve for Keq of step 1: Keq = [N₂O₄]/[NO₂]². Since we are trying to substitute for [N₂O₄] in the slow step's rate law, we should rearrange this Keq expression to equal [N₂O₄]. When doing this, you should get [N₂O₄] = Keq[NO₂]².

This may look confusing, but we are basically trying to find something to replace the intermediate with in the rate law. By setting up the fast equilibrium, we can place reactants into the rate law in place of the intermediate. Since [N₂O₄] = Keq[NO₂]², we can replace the [N₂O₄] in R = k[N₂O₄] with Keq[NO₂]².

This would give us the rate law of R = kKeq[NO₂]², which is consistent with the rate law before. You can kind of ignore the two different k values, as those aren't the point of emphasis in these questions. You can think of them as "k."

For reference, check out the given College Board sample response below:

Part c.ii Sample Response: Yes. Step 2 is slow; therefore, it is the rate-determining step of this mechanism. The rate law of this elementary reaction is rate = k[N₂O₄]. Because N₂O₄ is an intermediate, it cannot appear in the rate law of the overall reaction. Because Keq = [N₂O₄]/[NO₂]² in step 1, [N₂O₄] = Keq[NO₂]². Then, substituting Keq[NO₂]² for [N₂O₄] in the rate law of step 2 gives rate = (k Keq)[NO₂]², which is consistent with the rate law in part (b).

All given sample responses are provided by the College Board's Scoring Guidelines from the 2019 Exam Administration.

Browse Study Guides By Unit

⚛️Unit 1 – Atomic Structure & Properties

🤓Unit 2 – Molecular & Ionic Bonding

🌀Unit 3 – Intermolecular Forces & Properties

🧪Unit 4 – Chemical Reactions

👟Unit 5 – Kinetics

5.0Unit 5 Overview: Kinetics

5.1Reaction Rates

5.2Introduction to Rate Law

5.3Concentration Changes Over Time

5.4Elementary Reactions