Jillian Holbrook
AP Chemistry 🧪
269 resourcesSee Units
What is Cell Potential?
In the previous section, we explored the idea of electromotive force from redox reactions! Electromotive force is the “pull” on electrons from a reducing agent to an oxidizing agent. The higher the electromotive force is, the more spontaneous the reaction will be.
We can conceptualize electromotive force by generally thinking about how strongly each chemical species wants to either get rid of electrons or gain electrons. Although narrowing the scope to atoms or ions exchanging electrons this way is not always the most realistic representation, it can help us to visualize how electromotive force may work. Electromotive force, in units of volts, is a way to measure cell potential.
When dealing with a galvanic cell, the reduction and the oxidation occur on separate sides. The anode is the side where oxidation occurs, and the cathode is where reduction occurs. (Remember: An Ox; Red Cat)
Electrons travel through a wire from the anode to the cathode. The force these electrons experience as they pull through the wire is known as the cell potential. It is the same as the electromotive force caused by the redox reaction.
If a cell is under standard conditions, that means that the cell has 1 M concentrations and is at a temperature of 298 K and a pressure of 1 atm. We can calculate standard cell potential using the equation E°cell = Ecathode - Eanode. In other words, the standard cell potential for a cell is the reduction potential for the species in the cathode minus the reduction potential of the species in the anode.
Take a look at this example:
Calculate the cell potential for the following cell given the electrochemical data below:
2AgBr + 2Hg → 2Ag + Hg2Br2
Hg2Br2 + 2e- → 2Hg + 2Br- (E = +0.140 V)
2AgBr + 2e- → 2Ag + 2Br- (E = +0.071 V)
For this reaction, we see that AgBr reduces into Ag and Br-, so the cathode will be AgBr. At the anode, Hg oxidizes.
Plugging into our equation, we find that for E°cell = Ecathode - Eanode, E°cell = 0.071 V - 0.140 V = -0.069 V.
Another strategy for finding cell potential is to negate the oxidation reaction and then add the cell potentials together. For example, looking at the previous question, we could have also acknowledged that the actual half-reaction for Hg was 2Hg + 2Br- → Hg2Br2 + 2e-, which has a potential of -0.140 V. If we do E°cell = +0.071 V + (-0.140 V), the math yields the same result of -0.069 V.
Calculating Cell Potential Using Reduction Potentials
In the last problem, we were given specific electrochemical data, but for some questions, you will need to reference and apply values from a table of standard reduction potentials. Essentially, a table of standard reduction potentials is a very long list of reduction reactions with their corresponding potentials.
To find the correct value requires the right set of half-reactions, including which half-reaction occurs at the anode and which occurs at the cathode. Once we make these determinations, we can apply our cell potential equation: E°cell = Ecathode - Eanode.
The AP Exam will directly provide the necessary data to solve for cell potential. However, familiarity with a table of standard reduction potentials helps to build conceptual understanding, which is useful in practice and on testing day. Below is a sample table of standard reduction potentials:
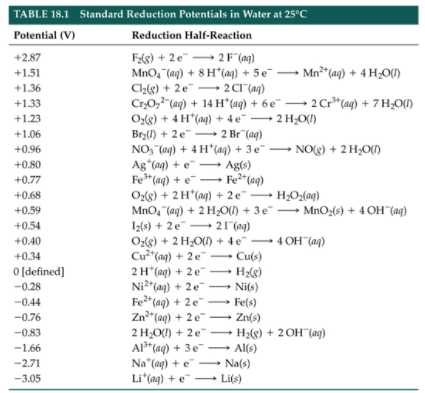
Image From Grade12UChem
Note that the reduction of H+ into H2 is a defined value of 0 V. This is because all other reduction potentials are modeled by comparing their voltage to the voltage of this reduction, essentially asking the question, “is this reaction more spontaneous or less spontaneous than 2H+ + 2e- → H2?”
The values in this table are all reductions, which is why we negate the potential if we manipulate the reactions to be oxidations. For many substances, the reduction has a negative potential. What does that mean? A negative reduction potential indicates that species like sodium (Na) and lithium (Li) are excellent reducing agents rather than species that are easy to reduce. If we flip the reductions in these cases, we see the negative reduction potentials become positive in the instance of oxidation, meaning oxidation is more favorable.
Standard Cell Potentials and Spontaneity 🔋
The major conclusion we want to draw from finding cell potential is the spontaneity and thermodynamic favorability of the redox reaction taking place. If E°cell is positive, the reaction is spontaneous. Why? The electromotive force is strong enough to pull the electrons off the reducing agent and onto the oxidizing agent. Conversely, if the E°cell is negative, the reaction is nonspontaneous. Therefore, we can predict the sign on ΔG° for a reaction given E°cell.
To reiterate:
If E°cell > 0, the reaction is spontaneous (thermodynamically favored), and ΔG° is negative.
If E°cell < 0, the reaction is nonspontaneous (thermodynamically unfavored), and ΔG° is positive.
Calculating ΔG° Using E°cell
While we can look at the sign on E°cell to predict the sign of ΔG°, we also have a way of directly calculating ΔG° from cell potential. The formula for ΔG° using E°cell is as follows:
ΔG° = -nFE°cell
In this equation, ΔG° is the standard Gibbs Free Energy change, E°cell is the standard cell potential, n is the number of moles of electrons transferred in the reaction, and F is Faraday’s constant, which is 96,485 coulombs/mol e-. A coulomb is a measure of electric charge.
We can take a look at the following example:
Suppose we have a galvanic cell for which E°cell = 1.02 V. In the reaction that occurs, 1 mol of electrons transfer. At 298K, what is ΔG° for this cell? What is the equilibrium constant, K?
First we can plug into ΔG° = -nFE°cell to find ΔG°:
ΔG° = -nFE°cell
ΔG° = -1(96,485)(1.02) = -98414.7 J = -98.414 kJ
Therefore ΔG° = -98414.7 J or -98.414 kJ.
Next, we can use our relationship between ΔG° and K to find the equilibrium constant:
K = e^(-ΔG°/RT)
K = e^(98414.7 /(8.314)(298)) = 1.78 * 10^17
Congratulations! Now you know how to calculate cell potential and how to apply cell potentials to calculate the standard change in Gibbs Free Energy.
Browse Study Guides By Unit
⚛️Unit 1 – Atomic Structure & Properties
🤓Unit 2 – Molecular & Ionic Bonding
🌀Unit 3 – Intermolecular Forces & Properties
🧪Unit 4 – Chemical Reactions
👟Unit 5 – Kinetics
🔥Unit 6 – Thermodynamics
⚖️Unit 7 – Equilibrium
🍊Unit 8 – Acids & Bases
🔋Unit 9 – Applications of Thermodynamics
🧐Exam Skills
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.