9.5 Free Energy and Equilibrium

In Unit 7, we spent a ton of time discussing the concept of equilibrium. Equilibrium helped us determine how a reversible reaction may behave under certain circumstances. In this section, we will look at how equilibrium connects to spontaneity and ΔG° by observing various definitions of equilibrium along with relationships between ΔG° (ΔG at standard conditions) and ΔG (ΔG at any other conditions). 

When learning about equilibrium, the typical definition is the kinetic definition of equilibrium. This definition concerns the rates of the forward and reverse reactions as the reaction approaches equilibrium. Recall that we defined equilibrium as the point at which the forward reaction and reverse reaction proceeded at the same rate, meaning the concentrations of products and reactants stay the same. It is important to note that equilibrium does not mean nothing is happening, just that both reactions are happening at the same rate, so they “cancel” each other out.

However, there is another important definition of equilibrium, which concerns thermodynamics (the thermodynamic definition). The thermodynamic definition defines equilibrium as the point of minimum free energy. While the reaction occurs spontaneously, ΔG (note the lack of the naught symbol: the ° next to G) will be less than zero, meaning the reaction will be releasing free energy. After it reaches equilibrium concentrations, ΔG will be positive and, thus, requires external sources of energy to occur.

We can see the point of minimum free energy visually in the following graphs, in which the y-axis is free energy (G), and the x-axis is the extent of reaction from 100% reactants to 100% products:

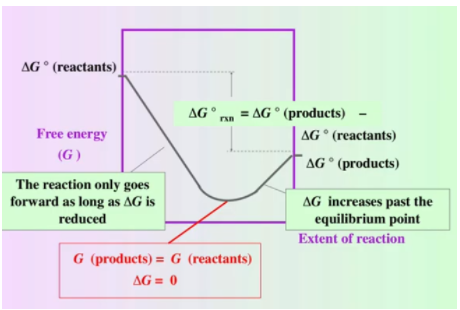
Whoa. What’s going on here? We can break down the graph above piece by piece.

First, note that ΔG is not the y position of the graph but rather the rate of change of the graph. When ΔG < 0, the graph decreases, and when ΔG > 0, the graph increases. 

We begin on the far left with 100% reactants, so ΔG = ΔG° of the reactants. Similarly, on the far right, we have 100% products, so ΔG = ΔG° of the products. We can see that the ΔG° of the products is lower than the ΔG° of the reactants, indicating that ΔG° for this particular reaction is negative and defines the reaction as spontaneous: ΔG° = ΣnΔG°f (products) - ΣnΔG°f (reactants).

For this reaction, we begin with a negative ΔG. The reaction is still in a spontaneous “state." Therefore, we will continue producing products. We move forward until we hit the point at which ΔG=0—the minimum point of free energy known as the equilibrium point.

From the equilibrium point forward, ΔG > 0. Thus, we need to add energy to the system to produce more products because the reaction is now nonspontaneous.

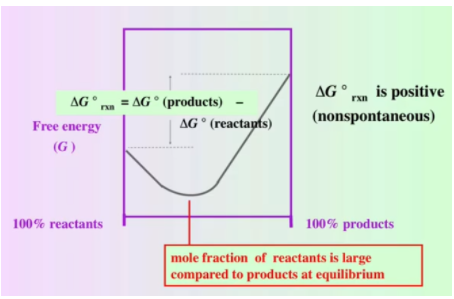
The above graph is similar to the graph from before. Except, note that our ΔG° (products) is now greater than ΔG° (reactants). Essentially, ΔG° is positive for this reaction and nonspontaneous. We are also told that the mole fraction of reactants is large compared to products at equilibrium, suggesting that we have many more reactants than products. A nonspontaneous reaction is linked to a reactant factored reaction.

After observing a qualitative relationship between ΔG°, ΔG, and K, we can look at some of the mathematical equations that are used to describe this relationship. Remember that ΔG is a measure of free energy change at nonstandard conditions, so a relationship can be drawn between ΔG° and ΔG by connecting it to Q, the reaction quotient:

To calculate Q, we plug non-equilibrium concentrations or pressures in the law of mass action (our equilibrium formula). R is the gas constant (8.314 J/molK or equivalent units), and T is the temperature in Kelvin. 

Next, we examine the relationship between ΔG° and K. Using our above equation, we can derive a relationship directly with only ΔG°. At equilibrium, the two main conditions are ΔG = 0 and Q = K. Substituting into our equation, we find the following:

0 = ΔG° + RTln(K)

Solving for K:

-ΔG° = RTln(K)

-ΔG°/RT = ln(K)

These two equations show a direct relationship between ΔG° and K. Qualitatively, we see that a higher ΔG° means a lower K and vice versa. With a positive ΔG°, we see that -ΔG°/RT is negative. Therefore, K is e^(negative number), making it less than 1. Similarly, with a negative ΔG°, -ΔG°/RT is positive, so K = e^(positive number) and greater than 1.