9.9 Cell Potential Under Nonstandard Conditions
5 min read•june 18, 2024
Jillian Holbrook
AP Chemistry 🧪
269 resourcesSee Units
In this unit, we have covered that chemical reactions in electrochemical cells can generate electricity. However, until now, we only looked at electrochemical cells under standard conditions. In an electrochemical cell, standard conditions are 298.15 K, 1 atm, a reaction quotient Q of Q =1, and, most importantly, 1 M concentrations of both solutions in either half-cell and Q = 1.
At standard conditions, we can calculate E°cell using standard reduction potentials. If the electrochemical cell is under nonstandard conditions, we have to make predictions as to whether the voltage of the nonstandard cell will be larger or smaller than E°cell. This section focuses entirely on interpreting Ecell and making connections to concentration, cell potential, and equilibrium.
Comparing Ecell and E°cell
You may remember in topic 9.5 that we discussed the difference between ΔH° and ΔH, including how ΔH is a driving force toward equilibrium. The same applies to Ecell and E°cell!
It is important to know that a galvanic cell that is running is not at equilibrium. Equilibrium arguments such as Le Châtelier’s principle, resultantly, do not apply to electrochemical systems.
By running, the cell is moving toward equilibrium, meaning the farther the reaction is from equilibrium, the
greater the magnitude of the cell potential. When the reaction enters dynamic equilibrium, the voltage at that nonstandard position will be zero—exactly what a dead battery is! A dead battery is nothing more than a galvanic cell that has reached equilibrium. At equilibrium, Ecell = 0.
Similar to ΔH° and ΔH, at equilibrium, ΔH = 0. Therefore, we can draw a relationship between Ecell and Q based on the relationship between ΔH and Q:
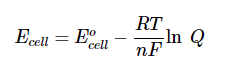
Image From LibreTexts
In this instance, R is 8.314 J/molK (or equivalent depending on units), T is temperature, n is moles of electrons, and F is Faraday’s constant, which is 96485C/ mol e-. This equation is known as the Nernst Equation and shows us the relationship between E°cell and Ecell and Q.
Concentration and Cell Potential
An important factor in predicting cell potential at nonstandard conditions is concentration. At standard conditions, solution concentration is always 1 M, but under nonstandard conditions, we can still make predictions as to what Ecell is like compared to E°cell.
We want to do this by remembering that at standard conditions, Q = 1 (this is because the concentrations are both 1, so [1]^n/[1]^m = 1) and that Q = [product]^n/[reactant]^m where n and m are stoichiometric coefficients. If Q > 1, we find that we have “too many products,” and thus, our Ecell will be less than E°cell. Similarly, if Q < 1, we find that Ecell will be greater than E°cell.
To solidify this concept, consider the following example:
Take the reaction 2Al (s) + 3Mn2+ (aq) → 2Al3+ (aq) + 3Mn (s) and compare Ecell to E°cell for the following scenarios:
- [Al3+] = 1.5M and [Mn2+] = 1.0M
- [Al3+] = 1.0M and [Mn2+] = 1.5M
- [Al3+] = 1.5M and [Mn2+] = 1.5M
For each of these parts, we will use the same method: finding Q, comparing it to Q = 1, and then drawing conclusions from that value.
In general, we can see that Q = [Al3+]^2 / [Mn2+]^3. Plugging in for problems 1-3, we find:
- Q = [1.5]^2 / [1.0]^2 > 1
- Q = [1.0]^2 / [1.5]^3 < 1
- Q = [1.5]^2 / [1.5]^3 < 1
For #1, we can conclude that Ecell < E°cell because Q > 1.
For #2 and #3, we can conclude that Ecell > E°cell because Q < 1.
Here is an additional multiple-choice example:
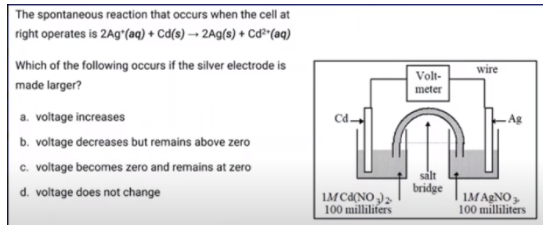
Image From Abigail Giordano
As always, we start with the Q expression for this reaction:
Q = [Cd2+]/[Ag+]^2
By making the silver electrode larger, neither of these concentrations changes. As long as there is an electrode, Q does not change in this instance. Therefore, the answer is D: Voltage does not change. If, instead, the Ag electrode was removed, our answer would be C.
Using the Nernst Equation
The Nernst Equation is another important way we can make predictions regarding the relationship between E°cell and Ecell. For a refresher, here are a few representations of the Nernst Equation:
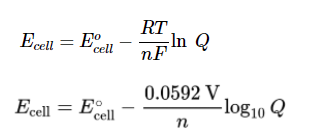
Image From LibreTexts
These are the same equation, except one is the natural log (log base e), and the other is log base 10. On the AP exam, you are NOT expected to use these equations to find actual values. Instead, the exam asks you to make predictions using the Nernst Equation.
These predictions will involve how a reaction will proceed given certain conditions for Ecell, E°cell, and Q. In understanding the Nernst Equation, we can draw predictions as to how changes in these values will affect the others.
Plugging in 0 for Ecell and K for Q, we can find a formula for E°cell at equilibrium:
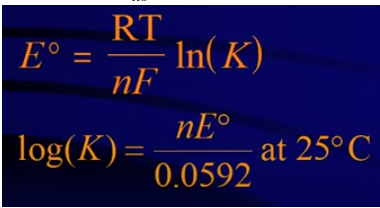
Image From Abigail Giordano
The cell potential is directly related to the Gibbs Free Energy (G) of a reaction occurring within the cell. Remember that Gibbs Free Energy is a measure of the energy available to do work and is defined as the difference between the enthalpy (H) and the product of the entropy (S) and the temperature (T) of the system, ΔG = ΔH - TΔS. The following chart examines these relationships laid out with the change in Gibbs Free Energy:
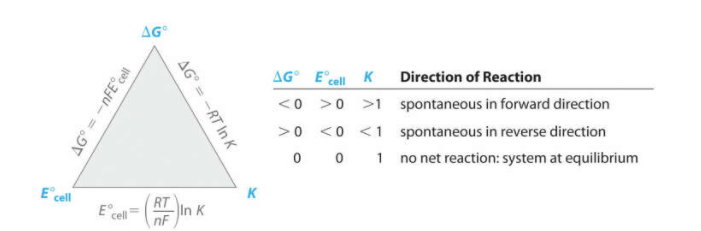
Nernst Equation Value 🧪
Ultimately, the Nernst Equation is a useful tool in chemistry for predicting the potential of an electrochemical cell under nonstandard conditions, such as when the concentration of reactants or products is not at standard concentrations. The Nernst Equation is based on the fundamental principles of thermodynamics and can be used to calculate the cell potential of an electrochemical cell under any set of conditions, including to:
- Predict the cell potential of an electrochemical cell at a given temperature.
- Determine the equilibrium constant of a chemical reaction at a given temperature.
- Calculate the concentration of reactants or products in an electrochemical cell at equilibrium.
- Determine the effect of a change in temperature on the cell potential of an electrochemical cell.
- Predict the potential of an electrochemical cell in a solution of nonstandard concentration.
Browse Study Guides By Unit
⚛️Unit 1 – Atomic Structure & Properties
🤓Unit 2 – Molecular & Ionic Bonding
🌀Unit 3 – Intermolecular Forces & Properties
🧪Unit 4 – Chemical Reactions
👟Unit 5 – Kinetics
🔥Unit 6 – Thermodynamics
⚖️Unit 7 – Equilibrium
🍊Unit 8 – Acids & Bases
🔋Unit 9 – Applications of Thermodynamics
🧐Exam Skills
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.