Recursion

4 min read•january 3, 2023

Milo Chang

AP Computer Science A 💻

130 resources

See Units

Recursion is a way to simplify problems by having a subproblem that calls itself repeatedly.

A recursive method has two parts: a base case and the recursive call. In the recursive call, the method basically calls itself, telling it to start over, either with the same parameters or different ones. After multiple calls, we approach the base case, where the recursion is stopped. Here is its anatomy:

public static void recursiveMethod()
  if (baseCaseCondition) { // base case
    base case steps
  } else {
    do something
    recursiveMethod(); // recursive call
  }
}

The Base Case

The base case is the last recursive call. When the base case is reached, the recursion is stopped and a value is returned. The base case is the easiest part of the recursive call to write and should be written first to make sure that the program doesn't run forever.

Recursive Calls and the Call Stack

Recursion involves a method calling itself with different parameter values until a base case is reached. The different recursive calls, or iterations of the method, are necessary to progress towards the base case. In order to write efficient recursive code, it is important to identify the subtask that the recursion is trying to solve, as well as the changes in the parameters that occur during each recursive call. Understanding these elements can help guide the implementation of the recursive method.

Whenever we have a recursive method, we have a call stack that keeps track of all the times that the recursive function is called, as well as their individual parameters. This is useful for when we have a function that has a recursive call in its return statement, where the results of later recursive calls are used in past calls. Here is a picture demonstrating the call stack for recursion.

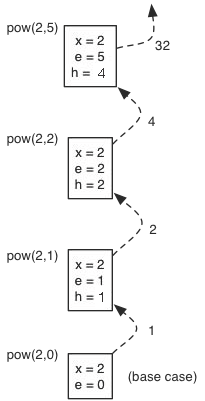
Courtesy of Cornell University.

In this, x and e are the parameters of the recursive calls, and h is the result of the recursion that is passed back up. The recursive calls are made from top to bottom, while the recursive returns are passed from bottom to top. This is where tracing comes in handy, as shown in the picture above!

Recursion vs. Loops

All recursion can be written as a loop, that is, all recursive code can be written iteratively.

If we can just use iteration, why use recursion?

The main answer? Simplicity. Recursive code is usually easier to read than iterative code.

Is there a trade-off? Yes. This comes in the form of speed and memory. This is because the call stack takes up memory in your computer when running the program, and it takes time to pass up the recursive return values.

Here is an example of an iterative and recursive method to do multiplication using repeated addition:

Iterative Code:

public static int multiply(int a, int b) {
  int sum = 0;
  for (int i = 0; i < b; i++) {
    sum += a;
  }
  return sum;
}

Recursive Code:

public static int multiply(int a, int b) {
  if (b == 0) {
    return 0;
  } else {
    return multiply(a, b - 1) + a;
  }
}

On the AP test FRQs, you can choose whether to write code iteratively or recursively, but you still have to know how recursion works for the AP exam! Writing recursive program code is outside the scope of the AP CSA course and exam.

Recursive Traversals

We can write ArrayList traversal using recursion. As a reminder, here is the iterative code:

for (int i = 0; i < arrayList.size(); i++) {
  System.out.println(arrayList);
}

Meanwhile, here is the recursive code:

public static void traverseArray(ArrayList<Integer> array, int startIndex) {
  if (startIndex == array.size() - 1) { // base case
    System.out.println(array.get(0));
  } else { // recursive case
    System.out.println(array.subList(startIndex, array.size()).get(0));
    traverseArray(array, startIndex + 1);
  }
}

//to use the above method
traverseArray(array, 0);

What This Method Is Doing

The recursion is actually getting the sublist of the big ArrayList with the first item in the sublist acting as the next item to be printed, and the last item in the sublist acts as the last item in the ArrayList.

The base case is when there is only one item left in the sublist, at which point the last item is printed and the method stopped.

We can also write recursive traversals of Strings and arrays.

Browse Study Guides By Unit

➕Unit 1 – Primitive Types

📱Unit 2 – Using Objects

🖥Unit 3 – Boolean Expressions & if Statements

🕹Unit 4 – Iteration

⚙️Unit 5 – Writing Classes

⌚️Unit 6 – Array

💾Unit 7 – ArrayList

💻Unit 8 – 2D Array

🖲Unit 9 – Inheritance