📚

All Subjects

💻

AP Comp Sci A

🖱

Unit 10

10.0 Unit 10 Overview: Recursion

10 min read•june 18, 2024

Kashvi Panjolia

AP Computer Science A 💻

130 resources

See Units

The Big Takeaway of this Unit

Recursion: We can use recursion in order to simplify repeated code and loops.

Exam Weighting

5-7.5% of the test
Roughly 2 to 3 multiple-choice questions

Enduring Understanding

Sometimes, you can break down a large problem or task by doing a subproblem repeatedly. This is called recursion. If this sounds like loops and iteration, it's because all recursive (the adjective form of recursion) methods can be written as a loop! We will learn how to use recursion effectively and see how this will simplify our code!

Building Computational Thinking

When writing recursion, notice how the code is much more simplified than if we were using loops. But, they will run slower, so we will sacrifice speed for conciseness in code. Recursive code has two main parts, the repeating/recursive part and the base case which makes sure we don't create an infinite loop in which our programs never stop.

Main Ideas for the Unit 💡

Intro to Recursion
How to Code Recursive Methods
Recursive Algorithms

10.1 Recursion

Recursion is a method of solving a problem where the solution depends on solutions to smaller instances of the same problem. It involves dividing the problem into smaller pieces, and calling the same function to solve each piece. The function calls itself with a smaller version of the original problem, and this process is repeated until the problem is small enough to be solved directly.

Each recursive method is comprised of a base case and a recursive call. A base case is a condition you want to check to terminate the method. It should be the last time the recursive method calls itself. A recursive call usually comes after the base case and is when a function calls itself with a modified version of the original problem. The base case and the recursive call work together to solve the problem. The recursive call breaks the problem down into smaller pieces, and the base case provides a way to solve the problem directly when it becomes small enough. The function keeps calling itself with smaller and smaller versions of the problem until it reaches the base case, at which point the recursion stops and the final result is returned. If the base case is not defined correctly, or if the function does not stop calling itself, it can lead to an infinite loop. 🔁

Here is an example of using recursion in Java to find the factorial of a number. The factorial of a number is the product of all the numbers from 1 to that number. So, the factorial of 5 (written as 5!) is 5 * 4 * 3 * 2 * 1, or 120.

public int factorial(int n) {

if (n == 1) {

return 1;

} else {

return n * factorial(n-1);

}

This function takes an integer n as an argument and returns the factorial of n. The base case is when n is equal to 1, in which case the function returns 1. For all other values of n, the function returns n multiplied by the factorial of n-1. Notice how the function calls itself inside the else statement, but modifies the argument being passed into it. This means, the else statement contains the recursive call. Even though there is a return statement inside the else statement, since the function is calling itself, the method will run again and again until the base case is reached, at which point the recursion stops and the final result is returned.

All recursive methods can be created using iteration. In some cases, iteration is more efficient than recursion, but in other cases, recursion is the better option. This is the factorial function written using a for loop:

public int factorial(int n) {

int result = 1;

for (int i = 1; i <= n; i++) {

result = result * i;

}

return result;

}

The second line creates a result variable to store the factorial of the number. The third line creates a for loop to iterate over the range of numbers from 1 to n, and multiplying the result by each number as it goes. The final result is returned after the loop finishes.

Recursion can also be used to traverse arrays and ArrayLists. Here is an example of how to traverse an array of integers using recursion:

public void traverseArray(int[] array, int index) {

if (index == array.length) {

return;

}

System.out.println(array[index]);

traverseArray(array, index + 1);

}

This function takes an array of integers and an index as arguments. The base case is when the index is equal to the length of the array, in which case the function simply returns and exits the recursive process. For all other values of the index, the function prints the element at that index and calls itself with an incremented index. This process is repeated until the base case is reached, at which point the recursion stops.

Compare the recursive method with the iteration method for traversal that you already know:

public void traverseArray(int[] array) {

for (int i = 0; i < array.length; i++) {

System.out.println(array[i]);

}

This version of the traverseArray method looks much simpler than the recursive version, which is why it is more widely used than the recursive version to traverse arrays. However, it is important to understand the recursive method of traversing arrays so you can practice using recursion.

10.2 Recursive Searching and Sorting

Binary search is an algorithm that allows you to search for an element in a sorted array by repeatedly dividing the search space in half. It is faster than linear search, which checks every element of the array until it finds the target element, and is what you have been doing to find if an element exists in an array. However, the array that the binary search is being used on must be pre-sorted from least to greatest. Binary search will not work if the array is not sorted before you call the binary search on it.

Here is an overview of how binary search works:

Set a lower bound low to the first element of the array and an upper bound high to the last element of the array.
Set a middle element mid to the average of low and high.
If the target element is equal to the element at mid, return mid.
If the target element is less than the element at mid, set the new high to mid - 1 and go back to step 2.
If the target element is greater than the element at mid, set the new low to mid + 1 and go back to step 2.
If the low index is greater than the high index, the target element is not present in the array, and the function returns -1.

Below is an iterative version of the binary search. Try to trace through the code so you understand how binary search works.

public int binarySearch(int[] array, int target) {

int low = 0;

int high = array.length - 1;

while (low <= high) {

int mid = (low + high) / 2;

if (array[mid] == target) {

return mid;

} else if (target < array[mid]) {

high = mid - 1;

} else {

low = mid + 1;

}

return -1;

}

This function takes an array of integers and a target element as arguments, and returns the index of the target element if it is present in the array, or -1 if it is not. It uses a while loop to repeatedly check the middle element of the search space and narrow down the search area until the target element is found or it is clear that the element is not present.

If the value we are trying to find in the array is higher than the middle element, the binary search method will stop looking at the values lower than the middle of the array. If the value is lower than the middle element, the binary search method will stop looking at the values higher than the middle of the array. Then, the binary search performs the same actions on that half of the array, and keeps cutting the array in half until an element is found to be a match, or returns -1 if the element is not in the array.

This is the recursive version of the binary search method. Again, try to trace the code to practice tracing and recursion.

public int binarySearch(int[] array, int target, int low, int high) {

if (low > high) {

return -1;

}

int mid = (low + high) / 2;

if (array[mid] == target) {

return mid;

} else if (target < array[mid]) {

return binarySearch(array, target, low, mid - 1);

} else {

return binarySearch(array, target, mid + 1, high);

}

The base case is when the low index is greater than the high index, in which case the function returns -1 because the lower index should always be less than the higher index. For all other cases, the function checks the middle element, and calls itself with modified bounds to search either the lower half or the upper half of the array depending on whether the target element is less than or greater than the element at mid.

As you can see, both the iterative and recursive versions of the binary search require about the same amount of effort, so the binary search method can be written using either structure.

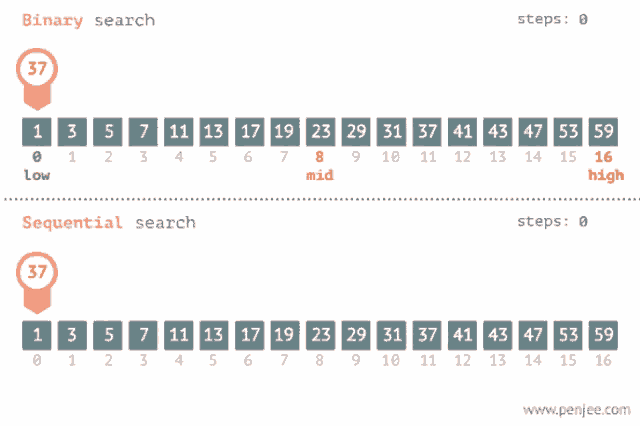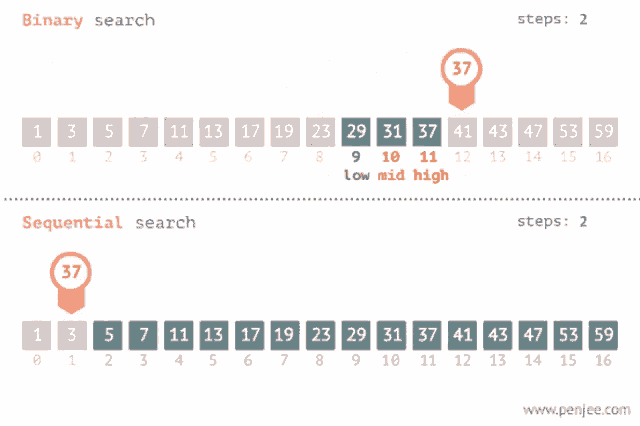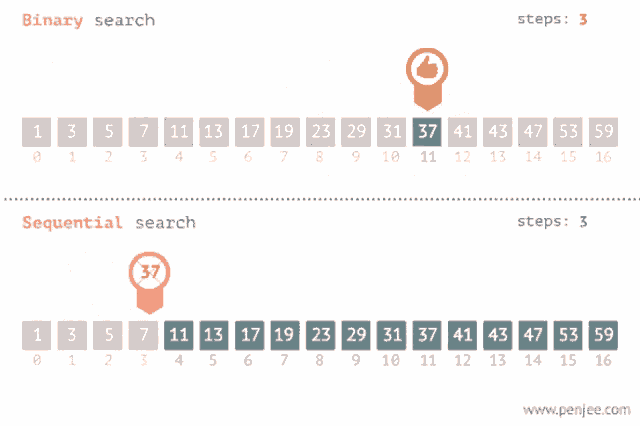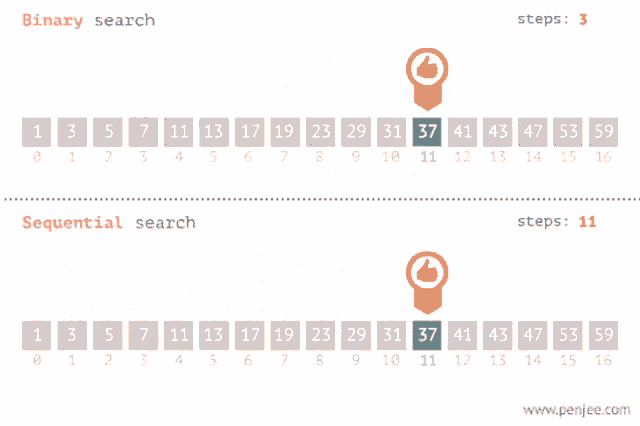
An example of how binary search uses fewer steps than sequential search. Image courtesy of Tenor.

Merge Sort

Merge sort is an efficient, general-purpose, comparison-based sorting algorithm. It works by dividing an array into two halves, sorting each half, and then merging the sorted halves back together.

This is the recursive version of the merge sort algorithm. It is a lot of code, but you have come this far in the AP CSA course, so you already know that taking it one block of code at a time will help you understand it.

public void mergeSort(int[] array) {

if (array.length > 1) {

// Split the array in half

int[] left = Arrays.copyOfRange(array, 0, array.length / 2);

int[] right = Arrays.copyOfRange(array, array.length / 2, array.length);

// Sort the halves

mergeSort(left);

mergeSort(right);

// Merge the sorted halves

merge(array, left, right);

}

public void merge(int[] result, int[] left, int[] right) {

// Merge the two sorted arrays into the result array

int i = 0;

int j = 0;

int k = 0;

while (i < left.length && j < right.length) {

if (left[i] < right[j]) {

result[k] = left[i];

i++;

} else {

result[k] = right[j];

j++;

}

k++;

}

// Copy any remaining elements of the left array

while (i < left.length) {

result[k] = left[i];

i++;

k++;

}

// Copy any remaining elements of the right array

while (j < right.length) {

result[k] = right[j];

j++;

k++;

}

The key to understanding how merge sort works is to recognize that it consists of two main steps: the divide step and the conquer step.

During the divide step, the array is divided into two halves. This is done by creating two new arrays, left and right, and copying the elements of the original array into them. The left array contains the elements from the beginning of the original array up to (but not including) the middle element, and the right array contains the elements from the middle element to the end of the original array.

Once the array has been divided, the conquer step begins. This step involves sorting the two halves of the array and merging them back together. The sorting is done by calling the mergeSort() function recursively on each half of the array. This causes the function to keep calling itself with smaller and smaller versions of the original problem until the base case is reached, at which point the recursion stops and the final result is returned.

The base case for the mergeSort() function is when the array has only one element, in which case it is already sorted and the function ends.

Once the two halves of the array have been sorted, they are merged back together using the merge() function. This function compares the elements of the two input arrays and inserts the smaller element into the result array. It continues this process until one of the input arrays is exhausted, at which point it copies the remaining elements of the other array into the result array.

The final result of the mergeSort() function is a sorted version of the original array.