📚

All Subjects

🎡

AP Physics 1

🌀

Unit 2

2.7 Applications of Newton’s Second Law

5 min read•june 18, 2024

Peter Apps

Daniella Garcia-Loos

AP Physics 1 🎡

257 resources

See Units

Linear Motion of a System ➰

The linear motion of a system can be described by the displacement, velocity, and acceleration of its center of mass. The variables x, v, and a, all refer to the center-of-mass quantities.

If you recall from kinematics there are a few major equations that relate acceleration, displacement, initial and final velocity, and time together.

Variable Interpretation: Δx is horizontal displacement in meters, Vf is the final velocity in meters/second, Vo is initial velocity in meters/second, t is time in seconds, and a is acceleration in m/s/s.

⟶ In order to solve for a variable without having all four other quantities known, we look at the ‘Variable Missing’ column to pick the equation that best suits our question.

Here are some tips for tackling application problems involving Newton's second law:

Identify the object of interest and draw a free-body diagram (FBD).
Identify all of the forces acting on the object. Be sure to include all forces, even those that may seem small or insignificant.
Determine the direction of the forces acting on the object. (Positive or Negative? Which way is down?)
Calculate the magnitudes of the forces acting on the object using the laws of physics, such as Newton's laws of motion or the principle of conservation of energy.
Use Newton's second law, F = ma, to solve for the unknown quantities in the problem, such as the acceleration of the object or the force required to move the object.
Check your solution to make sure it is reasonable and consistent with the problem statement. (The best way to do this is by checking to make sure the units make sense!)
If you are having trouble solving the problem, try breaking it down into smaller parts or identifying any constraints or assumptions made in the problem statement.

Important Acceleration Formulas 🗯

The acceleration is equal to the rate of change of velocity with time, and velocity is equal to the rate of change of position with time.

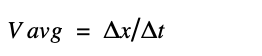
Equation:

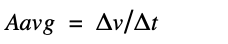
Angular Tension and Apparent Weight 🔊

Forces that the systems exert on each other are due to interactions between objects in the systems. If the interacting objects are parts of the same system, there will be no change in the center-of-mass velocity of that system.

Unfortunately, Newton’s Second Law also includes pretty infamous problems such as angular tension and apparent weight. Not to worry though, we’re going to break them down:

Key Concept: Angular Tension - mathematical problems when an object is held up by two or more strings at angles

Here are some steps for tackling an angular tension problem:

Identify the object of interest and draw a free-body diagram (FBD).
Identify all of the forces acting on the object, including the forces of tension.
Determine the direction of the forces of tension. In most cases, the forces of tension will act along the rope or cable, but they may also act at an angle.
Calculate the magnitudes of the forces of tension using the laws of physics, such as Newton's laws of motion or the principle of conservation of energy.
Use the magnitudes and directions of the forces of tension to solve for the unknown quantities in the problem, such as the angles between the rope or cable and the object, or the acceleration of the object.
Check your solution to make sure it is reasonable and consistent with the problem statement.

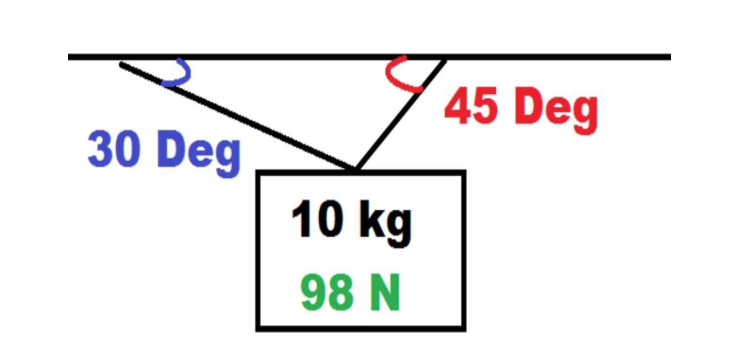
Image courtesy of VAM! Physics & Engineering.

🎥Watch: Organic Chemistry Tutor - Angular Tension

Key Concept: Apparent Weight - a property of objects that relates to how heavy an object is. The apparent weight of an object will be different from the true weight of an object when the Force of Gravity acting on that object is not balanced by an equal Normal Force.

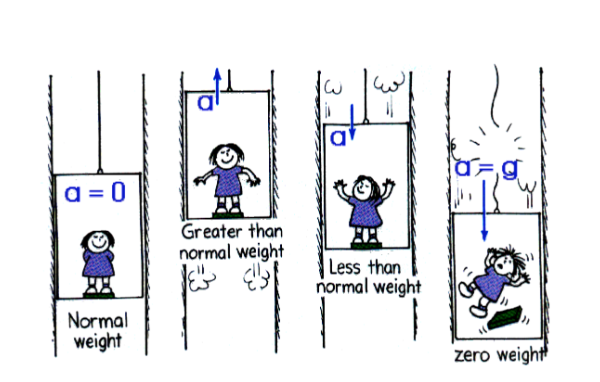
Image courtesy of physics.usask.ca

When you’re in an elevator going downwards and speeding up or going upwards and slowing down you tend to feel lighter. When you’re in an elevator going upwards and speeding up or going downwards and slowing down you tend to feel heavier. Why is that? To understand apparent weight fully, you must comprehend the four scenarios of the elevator problem:

When acceleration is upwards

The elevator accelerates upwards, but the inertia of a person would prefer to remain stationary, so the elevator floor must push up on the person with more force than their weight to accelerate them upwards. Therefore, Fn = ma + mg, so Normal Force is greater than true weight.

When acceleration is downwards

The elevator accelerates downwards, but the inertia of a person would prefer to remain stationary, so the elevator floor must drop out a little bit from underneath the person. This means the elevator floor must push up on the person less to support their weight, so Normal Force decreases. Therefore, Fn = mg - ma, so Normal Force is less than true weight.

When there is no acceleration

If the acceleration of an elevator is zero, the elevator is either moving with constant velocity or at rest. When this is the case Fn = mg, so Normal Force is equal to the true weight.

When an elevator is in free fall

If the elevator cable snaps, the elevator-person system will accelerate downwards at the rate of 9.8m/s/s (acceleration due to gravity). Since there is no contact between the floor of the elevator and the person Normal Force is zero. Therefore Normal Force is less than true weight.

Here are some steps for tackling an apparent weight problem involving an elevator:

Identify the object of interest and draw a free-body diagram (FBD).
Identify all of the forces acting on the object, including the force of gravity (weight) and the normal force.
Determine the direction of the forces acting on the object. The weight of the object will always act downward, while the normal force will act in the opposite direction, depending on the surface of the elevator.
Calculate the magnitudes of the forces acting on the object using the laws of physics, such as Newton's laws of motion or the principle of conservation of energy.
Use the magnitudes and directions of the forces acting on the object to solve for the unknown quantities in the problem, such as the acceleration of the elevator or the mass of the object.

🎥Watch: AP Physics 1 - Unit 2 Streams

Browse Study Guides By Unit

👟Unit 1 – Kinematics

🌀Unit 2 – Dynamics

2.0Unit 2 Overview: Dynamics

2.1Systems

2.2The Gravitational Field

2.3 Contact Forces

2.4Newton's First Law

2.5Newton's Third Law and Free-Body Diagrams

2.6Newton's Second Law

2.7Applications of Newton’s Second Law