Daniella Garcia-Loos
Erin Brzusek
AP Physics 1 🎡
257 resourcesSee Units
What is a System? 🌏
A system is an object or a collection of objects. Objects are treated as having no internal structure.
A system approach is often used to find the acceleration (F = ma, according to Newton’s Second Law of Motion) in which the total mass of the system is used.
Equation: ΣF = ma
Some key characteristics of a system include:
- A system has boundaries that define what is inside the system and what is outside the system. The boundaries of a system can be physical or conceptual.
- A system can exchange energy, matter, or both with its surroundings. The exchange of energy and matter between a system and its surroundings is known as an exchange of matter or energy.
- A system can be closed, meaning that it does not exchange matter or energy with its surroundings, or it can be open, meaning that it does exchange matter or energy with its surroundings.
- A system can be in equilibrium, meaning that it is not changing over time, or it can be in dynamic equilibrium, meaning that it is changing but is returning to a state of equilibrium after a period of time.
Fundamental particles are the building blocks of matter, and they are the smallest known units of matter. There are two main categories of fundamental particles:
- Subatomic particles are particles that are found within the nucleus of an atom, and they include protons, neutrons, and electrons.
- Particles that make up protons and neutrons are called quarks, and they are the smallest known units of matter. Quarks are held together by a force called the strong force, and they are found in protons and neutrons.
- Protons are made up of two types of quarks: up quarks and down quarks. Up quarks have a positive charge, while down quarks have a negative charge. When two up quarks and one down quark are combined to make a proton, the overall charge is positive.
- Neutrons are also made up of up quarks and down quarks, but the combination of these quarks results in a neutral charge. This is because the positive charges of the up quarks are canceled out by the negative charge of the down quark.
Example Problem #1:
A box is placed on a frictionless incline and is connected to a pulley system. The box has a mass of 10 kilograms, and the pulley has a mass of 2 kilograms. The tension in the rope is 50 newtons.
- What is the system in this scenario?
- What are the external forces acting on the system?
- Using Newton's second law, determine the acceleration of the box down the incline.
- If the incline angle is 30 degrees, what is the normal force acting on the box?"
1. The system in this scenario is the box and the pulley, along with the rope connecting them and the incline they are on.
2. The external forces acting on the system are the gravitational force acting on the box and the normal force acting on the box from the incline.
3. To determine the acceleration of the box down the incline, we can use Newton's second law, which states that the net force acting on an object is equal to the object's mass multiplied by its acceleration (F = ma). In this case, the net force acting on the box is the gravitational force minus the normal force, or F = mg - N, where m is the mass of the box, g is the acceleration due to gravity, and N is the normal force. The acceleration of the box is then (F/m) = (mg - N)/m.
4. If the incline angle is 30 degrees, we can use trigonometry to determine the normal force acting on the box. The normal force is equal to the weight of the box (mg) times the cosine of the angle between the incline and the horizontal plane. Therefore, N = mg*cos(30) = (10 kg)(9.8 m/s^2)*cos(30) = 49 newtons.
Example Problem #2:
Explain what a closed system is and provide an example.
To answer this question, you could explain that a closed system is a system that is completely isolated from its surroundings and does not exchange matter or energy with them. Then provide an example of a closed system, such as a sealed container filled with gas. The gas inside the container can interact with itself and the walls of the container, but it does not exchange matter or energy with the external environment. This makes the gas inside the container a closed system.
Properties of a System 🌟
Systems have properties that are determined by the properties and interactions of their constituent atomic and molecular substructures. In AP Physics, when the properties of the constituent parts are not important in modeling the behavior of the macroscopic system, the system itself may be referred to as an object.
Only external forces affect a system’s motion according to Newton’s First Law (an object at rest tends to stay at rest, and an object in motion tends to stay in motion). Because of this distinction, we must define the boundaries of a system before we can understand what forces are affecting its motion.
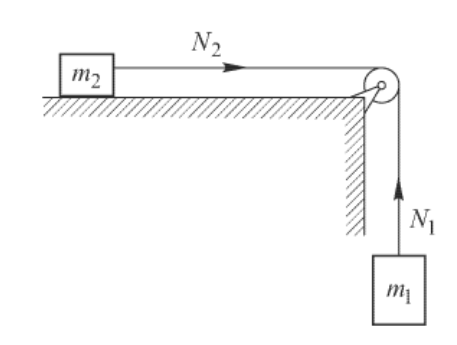
Image courtesy of physics.stackexchange.com
Illustrated in the image above, this particular system is comprised of a two-block pulley contraption with one of the blocks located on a table. A defining characteristic of a system is that the objects will accelerate together with the same magnitude. In addition, internal interactions such as tension have minimal changes or none at all which is why it can be regarded as a singular entity.
Example Problem:
Imagine you are studying a block of wood that is resting on a table. The block of wood is a macroscopic system, and it has various properties that can be used to describe and understand its behavior.
According to Newton's first law of motion, an object will remain at rest or in motion at a constant velocity unless acted upon by an external force.
What will happen to the block of wood if you apply a force to it? How will the properties of the block of wood, such as its mass, velocity, and acceleration, change as a result of the force being applied?
To answer this question, you might consider the following factors:
The magnitude of the force applied to the block of wood: A larger force will result in a larger acceleration of the block of wood.
The mass of the block of wood: A heavier block of wood will require a larger force to accelerate it to the same extent as a lighter block of wood.
The direction of the force applied to the block of wood: If the force is applied in the same direction as the block of wood's velocity, it will increase the velocity of the block of wood. If the force is applied in the opposite direction as the block of wood's velocity, it will decrease the velocity of the block of wood.
Browse Study Guides By Unit
👟Unit 1 – Kinematics
🌀Unit 2 – Dynamics
🚀Unit 3 – Circular Motion & Gravitation
⚡️Unit 4 – Energy
⛳️Unit 5 – Momentum
🎸Unit 6 – Simple Harmonic Motion
🎡Unit 7 – Torque & Rotational Motion
💡Unit 8 – Electric Charges & Electric Force
🔋Unit 9 – DC Circuits
🔊Unit 10 – Mechanical Waves & Sound
📚Study Tools
🧐Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.