Daniella Garcia-Loos
Erin Brzusek
AP Physics 1 🎡
257 resourcesSee Units
Types of Contact Forces ⛓
A contact force is a type of force that arises when two objects are in physical contact with each other. These forces can be either attractive or repulsive, and they arise due to the interaction between the particles that make up the objects. These forces will provide a foundation for the rest of this course, so get comfortable with them. And maybe brush up on your trigonometry!
Examples of contact forces include:
- Friction: This is a force that opposes the motion of an object when it is in contact with a surface. Friction is what allows us to walk on the ground, hold onto objects, and drive cars.
- Normal force: This is a force that acts perpendicular to a surface and supports the weight of an object resting on that surface. For example, when you sit on a chair, the chair exerts an upward normal force on you to support your weight.
- Tension: This is a force that acts along a rope or wire and is used to transmit a pulling force from one object to another. For example, when you pull on a rope to lift a heavy object, the rope exerts a tension force on the object.
Key Concept: Contact Forces - forces that occur when an object or system is in direct contact with another
Force | Description |
Tension | Occurs when an object is pulled by a rope, string, or chain |
Friction | Occurs when two surfaces are trying to slide (static) or sliding (kinetic) |
Normal | Occurs when an object is in contact with a surface |
Spring | Occurs when a spring or an elastic material is compressed or extended |
When creating free-body diagrams, we must understand how to correctly illustrate the direction of these contact forces.
- Tension - The direction the rope, string, or chain is attached
- Friction - opposes the direction of motion
- Normal - Perpendicular to the surface
- Spring - Opposes the direction of the extension or compression
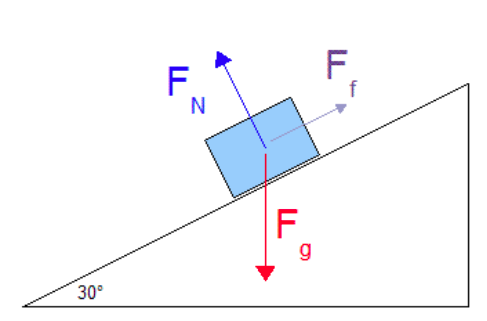
Image Courtesy of studyphysics.ca
The image above shows the free-body diagram of an object on an inclined plane, Weight is always drawn directly downwards. Friction is drawn opposite the direction of motion, and normal force is perpendicular to the surface.
🎥Watch: AP Physics 1 - Introduction to Forces Part 2
Things to remember about normal forces:
- A normal force is a force that acts perpendicular to a surface and supports the weight of an object resting on that surface.
- The normal force arises due to the interaction between the particles that make up the object and the surface it is in contact with.
- The normal force is always present when an object is resting on a surface.
- The normal force is important because it determines the amount of other forces that can act on an object. For example, the normal force determines the amount of friction that can act on an object.
Example Problem:
A box of mass 10.0 kg is placed on a ramp inclined at an angle of 30° to the horizontal. Calculate the normal force acting on the box.
To solve this problem, we can use the equation for the normal force, which is given by Fn = Fgcosθ, where Fn is the normal force, Fg is the gravitational force, and θ is the angle of the ramp. The gravitational force is given by the equation Fg = mg, where Fg is the weight and g is the acceleration due to gravity.
Plugging in the given values, we have: Fg = (10.0 kg)(9.80 m/s^2) = 98.0 N
The normal force is given by the equation Fn = Fgcosθ, so: Fn = (98.0 N)cos(30°) = 86.6 N
Therefore, the normal force acting on the box is 86.6 N.
Key Concept: Hooke’s Law - the amount of stretching or elongation of a string when a mass is attached to it is directly proportional to the applied weight.
Equation: F = -kx
- Where k is the spring constant in units of Newtons per Meter (N/m) and x is the stretching or elongation of the spring beyond its original length.
Example Problem: How much force is needed to pull a spring with a spring constant of 10 N/m a distance of 20 m?
Since we’re looking for the force required to pull the spring apart, we don’t need the minus sign!
F = 10 N/mᆞ20m Answer: The force needed is 200N |
🎥Watch: AP Physics 1 - Unit 2 Streams
Key Concept: Friction: A key factor in understanding the setup of the equations surrounding Newton’s Laws is familiarizing oneself with friction. Friction acts as the force that opposes the motion or attempted motion of an object.
The equation for friction is given by Ff <= μ*n where μ (Greek letter mu) is the coefficient of either static or kinetic friction. Friction is present if a problem mentions a “rough” surface, or specifically states the coefficient of static or kinetic friction.
Equation: Ff <= μ*n
Here are the main differences between static friction and kinetic friction:
- Static friction is the friction that acts on an object when it is not moving, or when it is in a state of static equilibrium.
- Kinetic friction is the friction that acts on an object when it is moving.
- Static friction acts to prevent an object from moving, while kinetic friction acts to oppose the motion of an object.
- Static friction is generally larger than kinetic friction. This means that it takes more force to start an object moving from rest than it does to keep it moving at a constant speed.
- Static friction is always present when an object is resting on a surface. Kinetic friction is always present when an object is moving on a surface.
- The amount of static friction and kinetic friction depends on the materials of the two surfaces in contact.
Example Problem:
A block of mass 4.00 kg is placed on a ramp inclined at an angle of 30° to the horizontal. The coefficient of friction between the block and the ramp is 0.400. Calculate the acceleration of the block as it slides down the ramp.
To solve this problem, we need to use the equation of motion F = ma, where F is the total force acting on the object, m is the mass of the object, and a is the acceleration. In this case, the total force acting on the block is the sum of the gravitational force, the normal force, and the force of friction.
The gravitational force is given by the equation Fg = mg, where Fg is the weight and g is the acceleration due to gravity. Plugging in the given values, we have:
Fg = (4.00 kg)(9.81 m/s^2) = 39.24 N
The normal force is given by the equation Fn = Fgcosθ, where Fn is the normal force, Fg is the gravitational force, and θ is the angle of the ramp. Plugging in the given values, we have:
Fn = (39.2 N)cos(30°) = 33.97 N
The force of friction is given by the equation Ff = μFn, where Ff is the force of friction, μ is the coefficient of friction, and Fn is the normal force. Plugging in the given values, we have:
Ff = (0.400)(33.97 N) = 13.59 N Parallel Component: this helps the block to slide down the ramp. This is calculated as: F(parallel) =mg sin(30°) = 4.00 x 9.81 x sin(30) = 19.62N The net force along the incline is the driving force for the block's acceleration:
F(net) = F(parallel) - F(f) = 19.62 - 13.59 = 6.03 N
Now, we can use the equation of motion F = ma to calculate the acceleration of the block:
a = F/m = (6.03 N)/(4.00 kg) = 1.51m/s^2
Therefore, the acceleration of the block as it slides down the ramp is 1.51 m/s^2.
FRQ PRACTICE: Want more practice with Friction? Check out this FRQ from the 2017 AP Physics 1 exam. |
Browse Study Guides By Unit
👟Unit 1 – Kinematics
🌀Unit 2 – Dynamics
🚀Unit 3 – Circular Motion & Gravitation
⚡️Unit 4 – Energy
⛳️Unit 5 – Momentum
🎸Unit 6 – Simple Harmonic Motion
🎡Unit 7 – Torque & Rotational Motion
💡Unit 8 – Electric Charges & Electric Force
🔋Unit 9 – DC Circuits
🔊Unit 10 – Mechanical Waves & Sound
📚Study Tools
🧐Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.