Kanya Shah
Jed Quiaoit
AP Statistics 📊
265 resourcesSee Units
Representations of Probability
Before we jump into the namesake subset of probability, let's review visual representations of probability.
There are several ways to visualize probability, including:
- Probability histograms: bar graphs that show the probability of different outcomes occurring; the x-axis represents the possible outcomes, and the y-axis represents the probability of each outcome.
- Plots: graphs that show the relationship between the probability of an event occurring and the value of a continuous random variable.
- Tree diagrams: diagrams that show the probability of different outcomes occurring in a series of events; each branch of the tree represents a different outcome, and the probability of each outcome is represented by the size of the branch. 🌲
- Venn diagrams: diagrams that show the relationship between different sets of outcomes; the area of each circle represents the probability of the corresponding set of outcomes occurring. 🔵
For this course, we'll focus on the last two on top of some old contenders like two-way tables.
Two-way tables and Venn diagrams can be particularly useful in calculating joint probabilities (the probability of two events occurring together) and conditional probabilities.
Tree diagrams are useful for visualizing the sample space of a chance process involving multiple stages, such as rolling a die and then drawing a card from a deck. They can help to understand the relationship between different outcomes and to calculate the probability of different sequences of events occurring. The probabilities shown on the branches of the tree are often conditional probabilities, calculated based on the probability of a previous event occurring.
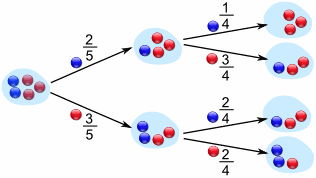
An example of a Tree Diagram
Image Courtesy of Pinterest
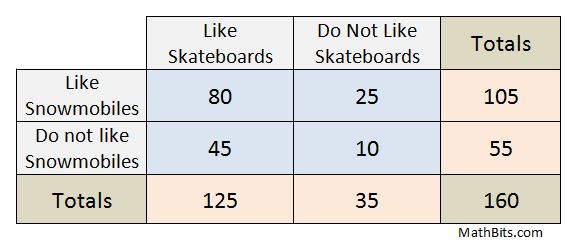
An example of a Two-Way Table
Courtesy of MathBits
Venn diagrams consist of one or more circles surrounded by a rectangle. Each circle inside the rectangle represents the sample space of the chance process.

An example of a Venn Diagram
Courtesy of Pinterest
Conditional Probability: Multiply and Divide!
Conditional probability is the probability of an event occurring given that another event has already occurred. It is often denoted by P(B | A), which represents the probability of event B occurring GIVEN that event A has already occurred.
The formula for calculating conditional probability is P(B | A) = P(A and B) / P(A), or
P(B | A) = P(A ∩ B) / P(A)
Vice versa: P(A | B) = P(A ∩ B) / P(B).
This formula can be rearranged to P(A and B) = P(A) * P(B | A). 📜
This is known as the general multiplication rule, which states that the probability of two events occurring together (P(A and B)) is equal to the probability of the first event occurring (P(A)) multiplied by the probability of the second event occurring given that the first event has already occurred (P(B | A)).
Similar to how unions have "OR" and intersections have "AND" as their magic words, the word "GIVEN" in a question is a good cue that'll give you a heads up on using conditional probabilities.
🎥 Watch: AP Stats - Probabilities: Two-Way Tables, Conditional, Independence, Tree Diagrams, etc
Practice Problem
A biotechnology company is developing a new gene therapy to treat a rare genetic disease. The therapy involves inserting a healthy copy of the gene into the patient's cells using a virus vector. The company has conducted clinical trials to determine the effectiveness of the therapy. 🧬
The clinical trial included 100 patients with the disease, and the results were as follows:
- 75 patients responded to the therapy (i.e., their symptoms improved)
- 25 patients did not respond to the therapy (i.e., their symptoms did not improve)
- 50 patients experienced side effects (i.e., adverse reactions)
- 50 patients did not experience side effects
The company wants to know (A) the probability that a patient will respond to the therapy, given that they experienced side effects and (B) the probability that a patient will not respond to the therapy, given that they did not experience side effects.
Answer
To solve this problem, you will need to calculate the conditional probabilities using the general multiplication rule.
(A) First, let's calculate the probability that a patient will respond to the therapy, given that they experienced side effects. This is represented by P(response | side effects).
To find this probability, we need to know the probability of the patient responding to the therapy (P(response)) and the probability of the patient experiencing side effects (P(side effects)).
Since 75 patients responded to the therapy out of 100 patients, the probability of a patient responding to the therapy is 0.75.
Since 50 patients experienced side effects out of 100 patients, the probability of a patient experiencing side effects is 0.5.
Using the general multiplication rule, we can calculate the conditional probability as follows:
P(response | side effects) = P(response) * P(side effects) = 0.75 * 0.5 = 0.375
This means that there is a 37.5% probability that a patient will respond to the therapy, given that they experienced side effects.
(B) Now, let's calculate the probability that a patient will not respond to the therapy, given that they did not experience side effects. This is represented by P(no response | no side effects).
Again, we need to know the probability of the patient not responding to the therapy (P(no response)) and the probability of the patient not experiencing side effects (P(no side effects)).
Since 25 patients did not respond to the therapy out of 100 patients, the probability of a patient not responding to the therapy is 0.25.
Since 50 patients did not experience side effects out of 100 patients, the probability of a patient not experiencing side effects is 0.5.
Using the general multiplication rule, we can calculate the conditional probability as follows:
P(no response | no side effects) = P(no response) * P(no side effects) = 0.25 * 0.5 = 0.125
This means that there is a 12.5% probability that a patient will not respond to the therapy, given that they did not experience side effects.
Practice Problem #2
A consumer research company is conducting a survey to understand the brand loyalty of customers in the clothing industry. They have collected data on 1000 customers who have purchased clothes from a particular brand within the past year.
The results of the survey are as follows: 👕
- 600 customers said they would definitely purchase from the brand again in the future
- 400 customers said they would consider purchasing from the brand again in the future
- 500 customers said they are satisfied with the brand
- 500 customers said they are not satisfied with the brand
The research company wants to know (A) the probability that a customer is satisfied with the brand, given that they would definitely purchase from the brand again in the future and (B) the probability that a customer is not satisfied with the brand, given that they would consider purchasing from the brand again in the future.
Answer
More conditional probability practice!
(A) First, let's calculate the probability that a customer is satisfied with the brand, given that they would definitely purchase from the brand again in the future. This is represented by P(satisfied | definitely purchase).
To find this probability, we need to know the probability of the customer being satisfied with the brand (P(satisfied)) and the probability of the customer definitely purchasing from the brand again in the future (P(definitely purchase)).
Since 500 customers are satisfied with the brand out of 1000 customers, the probability of a customer being satisfied with the brand is 0.5.
Since 600 customers would definitely purchase from the brand again in the future out of 1000 customers, the probability of a customer definitely purchasing from the brand again in the future is 0.6.
Using the general multiplication rule, we can calculate the conditional probability as follows:
P(satisfied | definitely purchase) = P(satisfied) * P(definitely purchase) = 0.5 * 0.6 = 0.3
This means that there is a 30% probability that a customer is satisfied with the brand, given that they would definitely purchase from the brand again in the future.
(B) Now, let's calculate the probability that a customer is not satisfied with the brand, given that they would consider purchasing from the brand again in the future. This is represented by P(not satisfied | consider purchase).
Again, we need to know the probability of the customer being not satisfied with the brand (P(not satisfied)) and the probability of the customer considering purchasing from the brand again in the future (P(consider purchase)).
Since 500 customers are not satisfied with the brand out of 1000 customers, the probability of a customer not being satisfied with the brand is 0.5.
Since 400 customers would consider purchasing from the brand again in the future out of 1000 customers, the probability of a customer considering purchasing from the brand again in the future is 0.4.
Using the general multiplication rule, we can calculate the conditional probability as follows:
P(not satisfied | consider purchase) = P(not satisfied) * P(consider purchase) = 0.5 * 0.4 = 0.2
This means that there is a 20% probability that a customer is not satisfied with the brand, given that they would consider purchasing from the brand again in the future.
Browse Study Guides By Unit
👆Unit 1 – Exploring One-Variable Data
✌️Unit 2 – Exploring Two-Variable Data
🔎Unit 3 – Collecting Data
🎲Unit 4 – Probability, Random Variables, & Probability Distributions
📊Unit 5 – Sampling Distributions
⚖️Unit 6 – Proportions
😼Unit 7 – Means
✳️Unit 8 – Chi-Squares
📈Unit 9 – Slopes
✏️Frequently Asked Questions
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.