4.8 Mean and Standard Deviation of Random Variables
5 min read•december 31, 2022
Kanya Shah
Jed Quiaoit
AP Statistics 📊
265 resourcesSee Units
Remember from previous sections that in statistics, a parameter is a numerical value that describes a characteristic of a population or the distribution of a random variable. It's a fixed value that is used to describe or summarize a population or sample. For example, the mean of a population is a parameter, as it describes the central tendency of the population. The standard deviation of a population is another example of a parameter, as it describes the spread or dispersion of the population. 🧞♂️
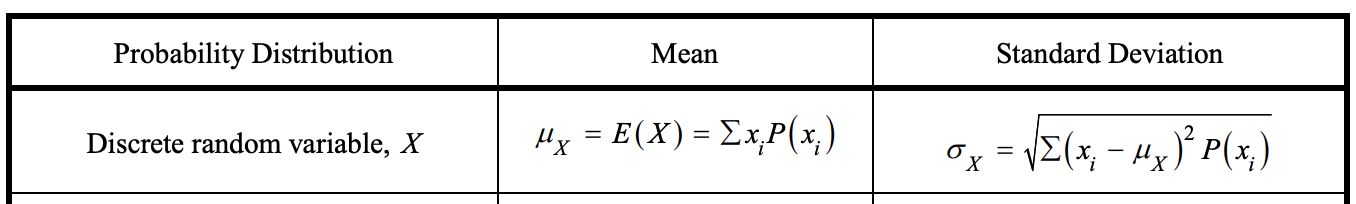
Credit: College Board
Center of a Discrete Random Variable
The mean or expected value of a discrete random variable is a measure of the central tendency of the variable. It represents the average outcome of the random variable over many repetitions of the same chance process.
To find the mean or expected value of a discrete random variable, X, you need to multiply each possible value of X by its probability and then add all of the products. This is often represented by the following formula:
E(X) = ∑x * P(X=x), where E(X) is the expected value of X, ∑x is the sum of all possible values of X, and P(X=x) is the probability of X being equal to x.
For example, if you have a discrete random variable X with two possible values, x1 and x2, and probabilities P(X=x1) and P(X=x2), respectively, then the mean or expected value of X would be:
E(X) = x1 * P(X=x1) + x2 * P(X=x2)
This gives you the average outcome of the random variable over many repetitions of the same chance process.
When calculating the mean or expected value of a discrete random variable, it is important to remember that the result is almost always a decimal value. This is because the probability of each possible value of the random variable is typically a decimal value.
For example, if you have a discrete random variable X with three possible values, x1, x2, and x3, and probabilities P(X=x1), P(X=x2), and P(X=x3), respectively, then the mean or expected value of X would be:
E(X) = x1 * P(X=x1) + x2 * P(X=x2) + x3 * P(X=x3)
If any of the probabilities, P(X=x1), P(X=x2), or P(X=x3), are decimals, then the expected value, E(X), will also be a decimal.
It is important to remember to write the expected value as a decimal, rather than rounding it to the nearest integer, as this can significantly affect the accuracy of your results.
Variability of a Discrete Random Variable
The standard deviation of a discrete random variable is a measure of the dispersion or spread of the variable's values around the mean. It tells you how much the values of the variable typically vary from the mean.
The variance of a discrete random variable, X, is a measure of the spread of the variable's values around the mean. It is calculated by taking the sum of the squares of the differences between each possible value of the variable and the mean, weighted by their probabilities. This is often represented by the following formula:
Var(X) = ∑(x - E(X))^2 * P(X=x), where Var(X) is the variance of X, ∑ is the sum of all possible values of X, E(X) is the mean or expected value of X, x is a possible value of X, and P(X=x) is the probability of X being equal to x.
The standard deviation of X is the square root of the variance, and is often represented by the following formula:
SD(X) = √Var(X), where SD(X) is the standard deviation of X and Var(X) is the variance of X.
So, to calculate the standard deviation of a discrete random variable, X, you would first calculate the variance using the formula above, and then take the square root of the variance to get the standard deviation. The standard deviation tells you how much the values of the variable typically vary from the mean, and a smaller standard deviation indicates that the values are more closely clustered around the mean, while a larger standard deviation indicates that the values are more spread out.
💡 AP tip: If you decide to use your calculator, make sure you list how you got to your answer. Use context and don’t just put a number down as the answer. Show work to maximize the amount of points you get.
🎥 Watch: AP Stats - Probability: Random Variables, Binomial/Geometric Distributions
Practice Problem
A random variable, X, represents the number of text messages a person receives in a day. The probability distribution of X is shown in the table below:

(a) Calculate the mean or expected value of X.
(b) Calculate the variance of X.
(c) Calculate the standard deviation of X.
(d) Interpret the results in the context of the problem.
Answer
To solve this problem, you would need to use the formulas for calculating the mean, variance, and standard deviation of a discrete random variable.
(a) To calculate the mean or expected value of X, you would need to multiply each possible value of X by its probability and then add all of the products. Using the formula E(X) = ∑x * P(X=x), you would get:
E(X) = (0 * 0.2) + (1 * 0.3) + (2 * 0.4) + (3 * 0.1) = 1.4
So, the mean or expected value of X is 1.4.
(b) To calculate the variance of X, you would need to take the sum of the squares of the differences between each possible value of the variable and the mean, weighted by their probabilities. Using the formula Var(X) = ∑(x - E(X))^2 * P(X=x), you would get:
Var(X) = (0 - 0.8)^2 * 0.2 + (1 - 0.8)^2 * 0.3 + (2 - 0.8)^2 * 0.4 + (3 - 0.8)^2 * 0.1 = 1.2
So, the variance of X is 1.2.
(c) To calculate the standard deviation of X, you would need to take the square root of the variance. Using the formula SD(X) = √Var(X), you would get:
SD(X) = √1.2 = 1.09544512
So, the standard deviation of X is 1.10.
(d) The mean or expected value of X is 1.4, which tells us that, on average, a person receives 1.4 text messages per day. The variance of X is 1.2, which tells us that the values of X tend to vary somewhat from the mean. The standard deviation of X is 1.10, which tells us that the values of X tend to be relatively closely clustered around the mean. This suggests that the number of text messages a person receives in a day tends to be relatively consistent, with relatively few extreme deviations from the mean.
Browse Study Guides By Unit
👆Unit 1 – Exploring One-Variable Data
✌️Unit 2 – Exploring Two-Variable Data
🔎Unit 3 – Collecting Data
🎲Unit 4 – Probability, Random Variables, & Probability Distributions
📊Unit 5 – Sampling Distributions
⚖️Unit 6 – Proportions
😼Unit 7 – Means
✳️Unit 8 – Chi-Squares
📈Unit 9 – Slopes
✏️Frequently Asked Questions
✍️Free Response Questions (FRQs)
📆Big Reviews: Finals & Exam Prep

Fiveable
Resources
© 2023 Fiveable Inc. All rights reserved.