Kanya Shah
Jed Quiaoit
AP Statistics 📊
265 resourcesSee Units
Intersections and Mutually Exclusive Events
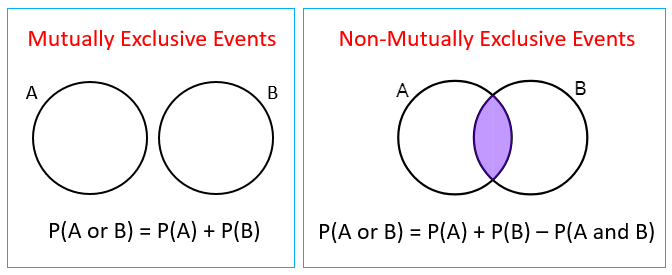
The intersection or joint probability of two events, denoted by P(A and B) where A and B are two events, is the probability of both events occurring simultaneously. It is composed of all outcomes that are common to both events. If two events are mutually exclusive, it means that they have no outcomes in common and cannot occur at the same time, so the probability of their intersection is 0. ☂️
INTERSECTION: P(A ∩ B) or P(A and B) (= 0 when mutually exclusive)
The addition rule for mutually exclusive events states that the probability of one or the other event occurring is equal to the sum of the probabilities of the individual events. This rule is based on the fact that if two events are mutually exclusive, it means that they cannot occur at the same time and have no outcomes in common, so the outcomes of one event cannot be included in the outcomes of the other event.
The addition rule for mutually exclusive events is often written as: ➕
P(A or B) = P(A ∪ B) = P(A) + P(B)
This equation states that the probability of event A or event B occurring is equal to the probability of event A occurring plus the probability of event B occurring. This rule is useful for calculating the probability of one event occurring or the other event occurring, as long as the events are mutually exclusive.
Source: Online Math Learning
It's important to note that the addition rule for mutually exclusive events only applies when the events are indeed mutually exclusive. If the events are not mutually exclusive, the probability of their intersection (P(A and B)) will not be 0, and the addition rule will not hold as there are some overlap between the two events.
Mutually Exclusive vs. Independence
It's important to be able to distinguish between mutually exclusive events and independent events (we'll go into further detail about independence on section 4.6). For now, what you need to know is that mutually exclusive events are events that cannot occur at the same time and have no outcomes in common, while independent events are events that are not affected by the occurrence of other events.
🎥Watch: AP Stats - Probability: Two Way Tables, Conditional, Independence, Tree Diagrams, etc.
Practice Problem #1
A group of students is taking a statistics exam, and they are asked to solve a problem that involves calculating the probability of two events occurring simultaneously. The problem states that the probability of event A occurring is 0.2, and the probability of event B occurring is 0.3. The problem also states that events A and B are mutually exclusive.
Using the information provided, answer the following questions:
- What is the probability of event A and event B occurring simultaneously (hint: probability of their intersection)? Explain your reasoning.
- What is the probability of one or the other event occurring (hint: the probability of the union of events A and B)? Explain your reasoning.
- If events A and B are not mutually exclusive, how would your answers to questions 1 and 2 change? Explain your reasoning.
Answer
Events A and B are mutually exclusive, which means that they cannot occur at the same time and have no outcomes in common.
1. Events A and B cannot occur at the same time and have no outcomes in common. Therefore, the probability of their intersection is 0.
2. Let's apply the addition rule for mutually exclusive events! The probability of one or the other event occurring, or the probability of the union of events A and B, is 0.2 + 0.3 = 0.5. This is because the probability of event A occurring is 0.2 and the probability of event B occurring is 0.3, and these events are mutually exclusive.
3. If events A and B are not mutually exclusive, the probability of their intersection would not be 0, and the probability of the union of events A and B would not be equal to the sum of the probabilities of the individual events. This is because if events A and B are not mutually exclusive, it means that they can occur at the same time and have at least one outcome in common. In this case, the probability of their intersection would be greater than 0, and the probability of the union of events A and B would be equal to the sum of the probabilities of the individual events minus the probability of their intersection.
Practice Problem #2
You are planning to visit a carnival with your friends, and you want to know the probability of certain events occurring while you are there. The carnival has a Ferris wheel, a roller coaster, a fun house, and a cotton candy stand. You are interested in the following events:
Event A: Riding the Ferris wheel.
Event B: Riding the roller coaster.
Event C: Going through the fun house.
Event D: Buying cotton candy.
The probability of each event occurring is as follows:
P(A) = 0.5
P(B) = 0.2
P(C) = 0.2
P(D) = 0.1
- What is the probability of going through the fun house OR riding the roller coaster?
- Are any of the events described in this problem mutually exclusive? Explain your reasoning.
Answer
1. The probability of going through the fun house or riding the roller coaster, or the probability of their union, is 0.4 (40%). This is because the probability of going through the fun house is 0.2 and the probability of riding the roller coaster is 0.2, and these events are independent. Therefore, the probability of their union is calculated as P(C or B) = P(C) + P(B) = 0.2 + 0.2 = 0.4.
2. The events described in this problem are mutually exclusive. Going through the fun house, riding the roller coaster, and buying cotton candy are all mutually exclusive events because it is not possible to do all of these things at the same time.
Browse Study Guides By Unit
👆Unit 1 – Exploring One-Variable Data
✌️Unit 2 – Exploring Two-Variable Data
🔎Unit 3 – Collecting Data
🎲Unit 4 – Probability, Random Variables, & Probability Distributions
📊Unit 5 – Sampling Distributions
⚖️Unit 6 – Proportions
😼Unit 7 – Means
✳️Unit 8 – Chi-Squares
📈Unit 9 – Slopes
✏️Frequently Asked Questions
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.