4.7 Introduction to Random Variables and Probability Distributions

6 min read•december 31, 2022

Kanya Shah

Jed Quiaoit

AP Statistics 📊

265 resources

See Units

A random variable is a variable that can take on different numerical values depending on the outcome of a random event. The probability distribution of a random variable specifies the probabilities of each possible value that the random variable can take on. It's common to use capital letters to represent random variables, such as X or Y.

❓ Types of Random Variables

A discrete random variable can only take on a finite or countably infinite number of possible values of X. The probability of a discrete random variable is typically associated with individual values, rather than intervals, because the random variable can only take on specific, discrete values. Examples of discrete random variables include the number of heads that appear when flipping a coin three times, or the number of cars that pass through a particular intersection in a given hour.

A continuous random variable, on the other hand, can take on any value within a certain range. Generally, you use a density curve to find the probability of a continuous variable and the probability usually applies to an interval rather than individual values. Examples of continuous random variables include the height of a person, or the time it takes for a runner to complete a race.

To find the probability of a particular value or range of values for a continuous random variable, you can use a probability density function (PDF), which is beyond the scope of AP Stats (phew!). The probability of a continuous random variable is typically associated with an interval of values, rather than individual values, because it is possible for the random variable to take on any value within a certain range.

In both cases, the probabilities of all possible values of the random variable must sum to 1, as there is always a certain probability of some outcome occurring.

🫂 Probability Distributions = Best Friend!

When calculating probability for discrete random variables, it's helpful to know whether you should include the boundary value in your calculations. This is because the wording of the problem can sometimes be confusing and you may need to determine whether the boundary value is included or excluded.

For example, if you are asked to calculate the probability that a discrete random variable X takes on a value of "at least 3," you would need to include the value of 3 in your calculations. On the other hand, if you are asked to calculate the probability that X takes on a value of "no more than 3," you would need to exclude the value of 3 from your calculations.

One way to help clarify these types of problems is to draw a mini probability distribution chart that shows all of the possible values of the random variable X and their probabilities. This can help you visualize the problem and make it easier to determine which values to include or exclude in your calculations on top of phrases like at least, no more than, greater than, etc.

To calculate the probability of a discrete random variable X taking on a particular value n, you can use the formula P(X = n) or P(Xn). This formula gives you the probability of the random variable X taking on the value n. You can then use this probability to answer the question or solve the problem you are working on.

A sample probability distribution chart is shown below:

Value	x1	x2	x3	x4
Probability	p1	p2	p3	p4

You need to know how to represent a discrete random variable as a histogram or in a table. For the histogram, use the discrete random variable as the x-axis values and the probabilities for the y-axis values.

Interpretation & Context

When describing the shape of a discrete random variable, it can be helpful to talk about whether the graph is roughly symmetric, double-peaked, or single-peaked, as well as whether it is right-skewed or left-skewed. These characteristics can give you insights into the underlying probability distribution of the random variable.

Here are examples of conclusions drawn from the shape of a graph of a discrete random variable:

If the graph of a discrete random variable is roughly symmetric, it means that the values of the random variable are evenly distributed around the center of the distribution. This often indicates that the distribution is normal, or bell-shaped.
If the graph of a discrete random variable is double-peaked, it means that there are two distinct peaks in the distribution. This often indicates that there are two distinct groups of values that the random variable can take on.
If the graph of a discrete random variable is single-peaked, it means that there is only one peak in the distribution. This can indicate that there is a dominant group of values that the random variable is more likely to take on.
If the graph of a discrete random variable is right-skewed, it means that the values are concentrated on the left side of the distribution, with a long tail extending to the right. This often indicates that the distribution is skewed towards lower values.
If the graph of a discrete random variable is left-skewed, it means that the values are concentrated on the right side of the distribution, with a long tail extending to the left. This often indicates that the distribution is skewed towards higher values.

In addition to describing the shape of the distribution, it's also important to mention the center (mean) and measure of variability (standard deviation) of the distribution. These values can help you make conclusions about the distribution and how the values of the random variable are likely to behave. For example, the mean of the distribution can give you an idea of the most likely value that the random variable will take on, while the standard deviation can give you an idea of how spread out the values of the random variable are.

🎥 Watch: AP Stats - Probability: Random Variables, Binomial/Geometric Distributions

🧠 Example

A recent study found that the probability that a person will develop a certain type of cancer is 0.01. This probability is independent of all other persons. The table below shows the number of people in a group of 10 people and the probability that exactly that number of people in the group will develop this type of cancer:

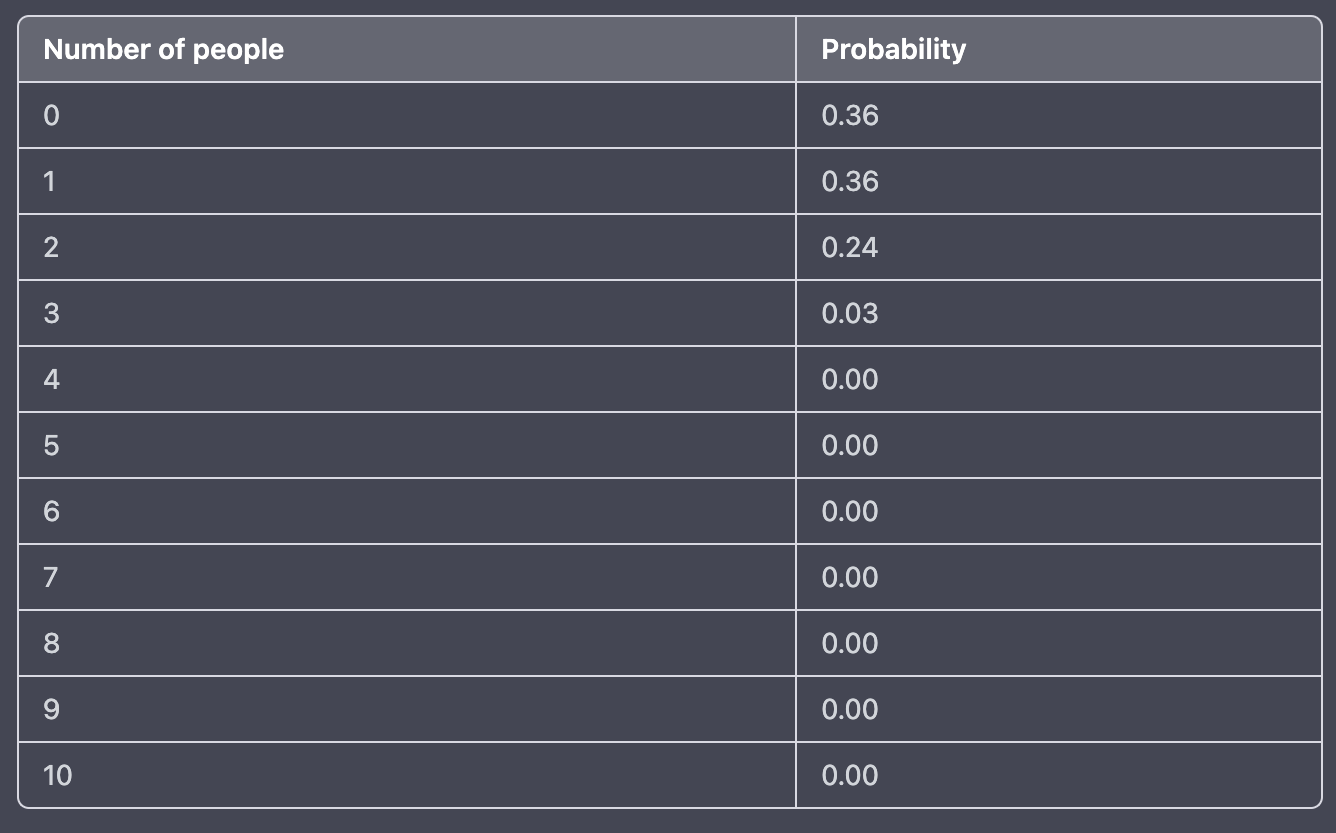
(a) What is the probability that at least 5 of a group of 10 people will develop this type of cancer?

(b) What is the probability that no more than 3 of a group of 10 people will develop this type of cancer?

(c) What is the probability that at most 2 of a group of 10 people will develop this type of cancer?

Answer

(a) To find the probability that at least 5 of a group of 10 people will develop this type of cancer, you will need to find the probability that exactly 5 people in the group will develop the cancer, plus the probability that exactly 6 people in the group will develop the cancer, plus the probability that exactly 7 people in the group will develop the cancer, and so on. You can do this by looking up the probabilities in the table and adding them all together.

P(X > 5) = 0.00 + 0.00 + 0.00 + 0.00 + 0.00 = 0.00

The probability that at least 5 of a group of 10 people will develop this type of cancer is 0.00.

(b) The probability that no more than 3 of a group of 10 people will develop this type of cancer is 0.96. This is calculated by adding the probabilities of exactly 0 people in the group developing the cancer (0.36), exactly 1 person in the group developing the cancer (0.36), and exactly 2 people in the group developing the cancer (0.24).

P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) = 0.36 + 0.36 + 0.24 = 0.96

The probability that no more than 3 of a group of 10 people will develop this type of cancer is 0.96.

(c) Same answer as (b).

Browse Study Guides By Unit

👆Unit 1 – Exploring One-Variable Data

✌️Unit 2 – Exploring Two-Variable Data

🔎Unit 3 – Collecting Data

🎲Unit 4 – Probability, Random Variables, & Probability Distributions